第１５０問の解答

１．問題　［空間図形、植木算］

問題図

半径が９ｃｍの球が、たくさんあります。
これを直径●ｃｍの円筒に３個入れたところ５０ｃｍの高さまで入りました。

では、直径が同じ●ｃｍの円筒で、高さが３７０ｃｍの筒にこの球を入れて、ふたをするとき、最大何個の球を入れることが出来るでしょうか。

　

２．解答例１( ありっちさん、mhayashiさん、MikiSugimotoさん、noetherさん、有無相生さん、清川育男さん、大岡敏幸さん、他多数)

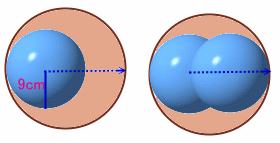
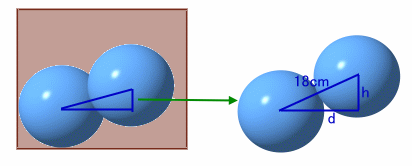
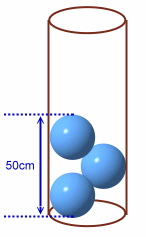
図１のように、１段目の球の上に２段目の球をおくとき、高さを低くするには２つの球を水平方向に最も遠い位置におく必要がある。

図１
参考図1		 図２
参考図2

このとき、底面（円）への射影（上方から見た図）で考えると、２つの円（球）の中心は、底面の同じ直径上にあり、それぞれ底面の円と接していることになる。

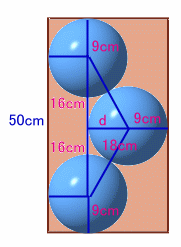
２段目の球の上に、３段目の球をおくときも同様であるため、３つの球の配置は、図２のようになる。
（d=√(182-162)=2√17≒8.25より、底面の直径=18+d≒26.25cm）

従って、球が１個増えるごとに（５０−９×２）／２＝１６ｃｍづつ高くなることが分かります。

よって、３７０ｃｍの高さにｎ個の球が入るとすると、
　１８＋(ｎ−１)×１６≦３７０
　ｎ−１≦（３７０−１８）／１６＝２２
　ｎ≦２３
従って、ちょうど２３個入ることになります。


答：２３個

以上

（参考問題）(たなかさん、中村明海さん、他)

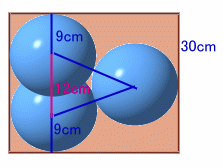
３個入れたときの高さが３０ｃｍのとき、１５０ｃｍの高さまでに
何個の球が入るでしょうか。

この問題になると、本問とは状況が違ってきます。
本問同様に考えると、１個球が増えたときに高さは
　（３０−９×２）／２＝６ｃｍ
づつ高くなることになります。

参考図3

しかし、これでは３個目の球が、１個目の球にめり込むことになるので、あり得ません。

とすると、２個目の球は１個目と同様に底面についてないと駄目ということになります。

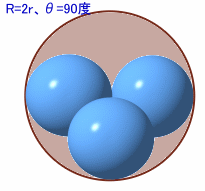
では、底面の直径Rが、球の半径r=9のちょうど２倍になったとしましょう。
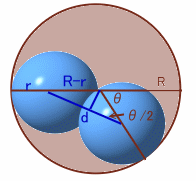
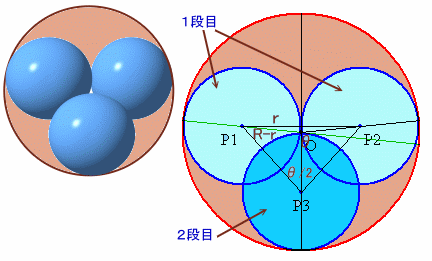
このとき、３個目の球をおいたときの高さは、いくらになるでしょうか。

これを求めるため、１個目と２個目の球の位置が次の図のようになるときの高さを求めてみましょう。

参考図4 参考図5

２つの球の中心の水平方向の距離は、
　ｄ＝２(Ｒ−ｒ)ｃｏｓ(θ/２)
となるので、中心の垂直方向の距離は、
　ｈ＝２√(ｒ2-(Ｒ−ｒ)2ｃｏｓ2(θ/２)）　・・・（１）
となります。

従って、Ｒ＝２ｒのとき、θ＝９０度なので、ｈ＝２√(ｒ2-ｒ2/２）＝ｒ√２≒１２．７３、よって筒の高さは１８＋１２．７３＝３０．７３ｃｍとなり、３０ｃｍをわずかながら越えます。

参考図6

従って、Ｒ＞ｒでなければなりません。

参考図7

上図のように配置すると、ｓｉｎθ＝ｒ/（Ｒ−ｒ）となります。
ｃｏｓθ＝２ｃｏｓ2（θ/2）−１より、
　ｃｏｓ2（θ/2）＝（１＋ｃｏｓθ）／２。
よって、１２＝２√(ｒ2-(Ｒ−ｒ)2（１＋ｃｏｓθ）/２）
　３６＝ｒ2−(Ｒ−ｒ)2（１＋ｃｏｓθ）/２
　(Ｒ−ｒ)2（１＋ｃｏｓθ）＝（８１−３６）×２＝９０

　ここで、(Ｒ−ｒ)2＝ｘとおくと、
　ｃｏｓθ＝（９０−ｘ）／x
よって、
　１−ｒ2／ｘ＝（９０−ｘ）2／ｘ2
　ｘ2−８１ｘ＝９０2−２・９０ｘ＋ｘ2
　ｘ＝９０2／９９

よって、Ｒ＝９＋√（９０2／９９）＝９＋３０／√１１≒１８．０５cm。

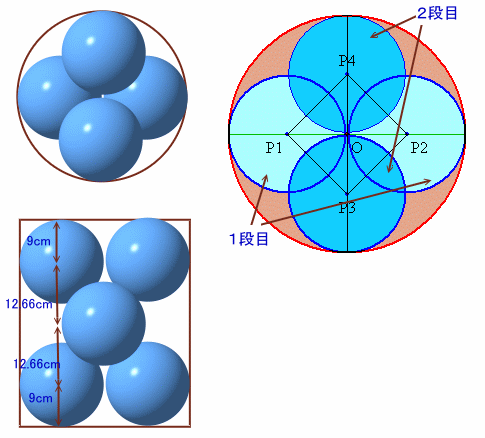
次に、１５０ｃｍまでの高さに入れていくときは、１段目の２つの球を底面の直径上に配置し(わずかな隙間あり)、２段目にはこれと直交するように２つの球を配置するようにすれば、効率的に積んでいける。

参考図8

１段増えるごとに増加する高さｈは（１）より、
　ｈ＝２√(９2-(３０／√１１）2（√２／２）2）
　　＝４２／√１１
　　≒１２．６６ｃｍ
となるので、１５０ｃｍまでにｎ段積めるとすると、
　１８＋（ｎ−１）×１２．６６≦１５０
　ｎ−１≦（１５０−１８０）／１２．６６≒１０．４２。

よって、ｎ≦１１となり、１１段まで積むことが出来ます。
１段につき２つの球を積めるので、全体では１１×２＝２２個の球をおけることとなります。

なお、２２個まで積めることは分かりましたが、２３個以上積むことができないことを実際に示すのは、なかなか難しいようです。

以下は、たなかさんが算チャレ掲示板に掲載された説明を、そのまま紹介させていただきます。

元の高さ30cm,150cmの場合の問題ですが、私も最大で22個までしか積めないことを確認しました。計算は一部省略しますが、一応概略を書いてみることにします。

円筒の半径をr+9とします。
既に議論されている内容から、半径30/Sqrt(11)+9のときは30cmに3個積めますので、r<=30/Sqrt(11)です。（おそらくイコールでしょうが、これは証明には使いません）

円筒を、
　{(x,y,z) ; x^2 + y^2 <= (r+9)^2, 0 <= z <= 150}
と書くことにします。

問題文より条件１：
任意のsについて、高さs <= z < s+12 の範囲に球の中心は3個以上 在しない（存在すると、rがもっと小さく取れることになってしまい、矛盾する）

さて、そこで円筒を以下の12個の部分に分割します。
　9<=z<21 , 21<=z<33 , ... , 129<=z<141 , z=141
条件１より、これらの中には高々２個しか球の中心は存在しません。
（もちろん、z<9,z>141にも存在しません。ここまでで、25個以上は不可能なことがわかります）

ここで、ある整数n(0,1,...,11)に対し、z=12n+9上に球の中心が存在しないと仮定します。
すると、z=12n+9より大きい部分について、
　12n+9<z<=12n+21 , 12n+21<z<=12n+33 , ... , 129<z<=141
と分割を変えると、z=12n+9より小さい部分と合わせて11個の部分に分割できたことになり、それぞれの部分には２個までしか置けないので23個以上置けません。

したがって、条件２：
23個以上置くためには、全てのn=0,1,...,11に対して、z=12n+9上に少なくとも１個は球の中心がなければなりません。
（ここまでの議論はrの具体的な数値は不要です）

ここからはあらすじのみになりますが・・・

さて、ここで２個球の中心が入っている12n+9<=z<12n+21の領域を考えます（23個入るためには１ヶ所以外は２個入らなければならない）
この領域には、条件２より、z=12n+9に中心が１つ、領域の外のz=12n+21にも中心が１つあります。領域内の中心のもう１つがz=12n+9+hにあるとします。
これらの３つの中心は互いに18cm以上離れていなければなりません。
この事実より、これらの中心をxy平面に投影したときに、原点とのなす角はある値以上でなければならないことがわかります。
その角度を具体的に計算してみると、z=12n+9とz=12n+9+h上の中心のなす角は
tan t = (Sqrt(1296-4h^2-104976/r^2+648h^2/r^2-h^4/r^2))r / (324-h^2-2r^2)
を満たすtとなります。
そこで、この角度とz=12n+9+hとz=12n+21上の中心のなす角、z=12n+9とz=12n+9+h上の中心がなす角の和(f(h)とします)が360度以下になるという条件式を立てます。
これは12n+9<=z<12n+21の範囲にはz=12n+9しか解を持ちません。
(f(n)を微分していくと、上に凸であることがわかります)

このことより、各領域に２個入っているとしたら、z=12n+9上に２個あることがわかりました。

ところがもし23個あったとすると、隣り合う領域で両方とも2個という場所が必ずあるはずですが、この場合、z=12n+9とz=12n+21の両方に２個ずつ中心があることになり、これは上記の角度の関係上不可能であることが解ります。

したがって、23個以上置くのは不可能であることが解ります。