第152問の解答
1.問題 [場合の数]
|
A、B、C、D、Eの5つの文字を左から順に1個ずつ選んで並べていきます。 さて、5個の文字を並べ終わったときに記録されている数字の和が奇数となるような並べ順は、何通りあるでしょうか。 |
2.解答例1( 高橋道広さん、まるケンさん、ヒデー王子さん、中村明海さん、あまれっとさん、素人では最年長?さん、他多数)
5個の文字を並べる方法は、5!=5×4×3×2×1=120通りあります。
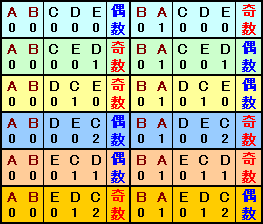
このうち、最初の2文字が同じもの(例えばA、B、*、*、*)を1まとめにして考えると、全部で5×4=20組、そして1組にはそれぞれ3×2×1=6通りの並べ方があります。
この20組をA、B、*、*、*およびB、A、*、*、*のように最初の2文字がちょうど入れ替えたものとなる2組をペアにして考えます。このようなペアは、20/2=10ペアあります。
さて、任意のペアX、Y、*、*、*およびY、X、*、*、*について考えます。
(ただし、XはYよりアルファベット順で前にあるとします)後ろの3文字が同じU、V、Wのとき、X、Y、U、V、WおよびY、X、U、V、Wでは、U、V、Wを並べるときに記録する数字は同じです。
また、X、Yでは0、0、そしてY、Xでは0、1となりますから、記録した数字の和は一方が奇数で、もう一方が偶数となります。従って、X、Y、*、*、*の6通りで記録した数字の和が奇数のものがn1、偶数が6−n1通りとすると、Y、X、*、*、*では、逆に偶数のものがn1、奇数が6−n1通りになります。(n1=3なのですが、そのことを今回は使いません)
すると、このペア全体では、奇数、偶数ともn1+(6−n1)=6通りになります。
(例)
全部で10ペアあったのですから、記録した数字の和が奇数のものは合計6×10=60通りとなります。
答:60通り
以上
他の解法としては、
・置換の問題に帰着する:noetherさん、ふぇるまーさん、あんみつさん
・帰納法によるもの:みずなぎさん、けむしろうさん
・数え上げによる:AUさん、有無相生さん、年中行灯さん
があります。