第153問の解答
1.問題 [平面図形]
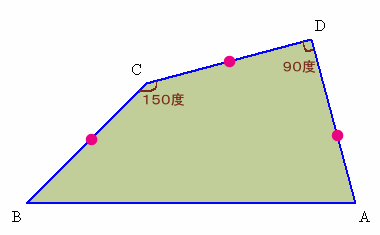 |
|
2.解答例1(トトロ@Nさん、たこやき大学さん、あんみつさん、みずなぎさん、大岡敏幸さん、吉川裕貴さん、他多数)
四角形CEADが正方形となるように点Eをとります。
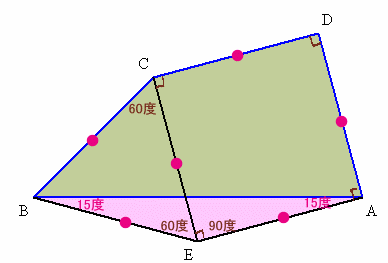
△CBEは、BC=CEより二等辺三角形。
∠BCE=∠BCD−∠ECD=150−90=60度。よって、△CBEは正三角形となり、BC=CE、∠BEC=60度。
△BEAは、BE=EAより、二等辺三角形。
∠BEA=∠BEC+∠CEA=60+90=150度。よって、∠EAB=(180−150)/2=15度。
従って、∠BAD=∠EAD−∠BAE=90−15=75度となります。
答:75度以上
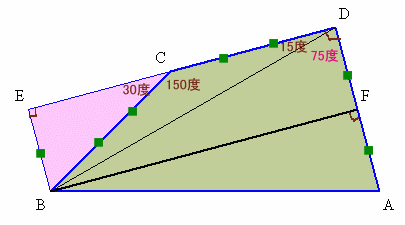
3.解答例2( 川田智之さん、他)
BからADと平行に引いた線分とDCの延長線との交点をE、
BからCDと平行に引いた線分とADの交点をFとします。
∠BEC=∠CDA=90度、∠BCE=180−∠BCD=30度。
よって、BE=BC×1/2。四角形BEDFは長方形となるので、DF=BE=AD×1/2。
よって、AF=DF=AD×1/2。従って、△BDAは二等辺三角形。
ところで、△BCDは二等辺三角形より、∠CDB=(180−150)/2=15度。
よって、∠BAD=∠BDA=90−15=75度となります。
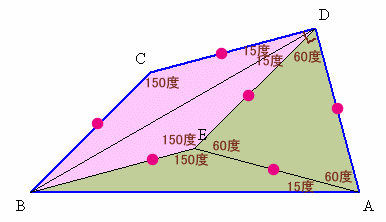
4.解答例3(あまれっとさん、他)
四角形BCDEが平行四辺形(菱形)となるよう点Eをとります。
△BCDは二等辺三角形で∠BCD=150度より、∠BDC=15度。
同様に、△BEDは二等辺三角形で∠BED=150度より、∠BDE=15度。よって、∠EDA=90−(15+15)=60度。
ED=ADより、△EDAは正三角形。
よって、∠DAE=∠DEA=60度。△BEAは二等辺三角形で∠BEA=360−(150+60)=150度より、∠EAB=15度。
従って、∠BAD=∠EAB+∠DAE=15+60=75度となります。
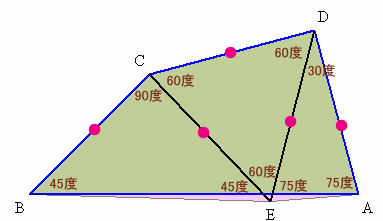
5.解答例4(高橋道広さん、mitchさん、他)
△CDEが正三角形となるよう点Eをとります。
BC=EC=ED=EAより、△BCEと△EDAは二等辺三角形。
∠BCE=150−60=90度より、∠BEC=45度。
∠EDA=90−60=30度より、∠DAE=∠DEA=75度。∠BEC+∠CED+∠DEA=45+60+75=180度。
よって、B、E、Aは一直線上にあることになり、
∠A=∠DAE=75度となります。
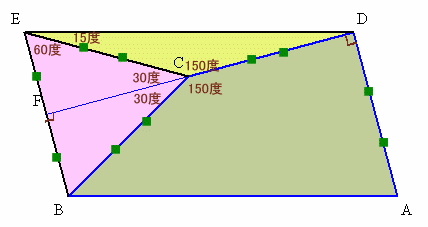
6.解答例5(うっしーさん、他)
四角形BEDAが平行四辺形となるよう点Eをとります。
また、DCの延長線とBEの交点をFとします。
∠BCF=180−150=30度、∠BFC=∠CDA=90度より、
BF=BC×1/2。BE=AD=BCより、EF=BF=BC×1/2。
よって、△BCEは正三角形となります。△ECDは二等辺三角形で∠ECD=360−(150+60)=150度。
よって、∠CED=15度。よって、∠A=∠BED=∠BEC+∠CED=60+15=75度となります。
7.解答例6(ET2世さん、他)
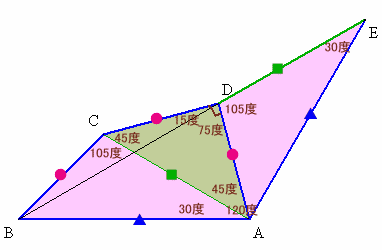
△ABCと同じ三角形を辺ADにつくり、△EADとします。
△BCDは二等辺三角形で∠BCD=150度より、∠BDC=15度。
よって、∠BDA=90−15=75度。△EAD≡△ABCより、∠ADE=∠BCA=150−45=105度。
よって、∠BDA+∠ADE=75+105=180度となり、B、D、Eは一直線上にあることになります。
従って、△BAEはAB=EAとなり、二等辺三角形。
∠BAE=∠BAD+∠DAE=∠BAD+∠CBA=360−(150+90)=120度。
よって、∠DEA=(180−120)/2=30度。
∠A=∠BAC+∠CAD=∠DEA+∠CAD=30+45=75度となります。