第１５４問の解答

１．問題　［速さの問題］

　Ａ君とＢ君の家は道のりにして８ｋｍ離れています。
　ある日、Ｂ君と会う約束をしていたＡ君は、自分の家を時速v1kmの自転車で出てＢ君の家に行き、Ｂ君の家の門が閉まっていたので、すぐに自分の家まで引き返しました。
　実は、Ｂ君も時速v2kmのバイクに乗ってＡ君の家に出かけたのですが、往路のＢ君の家から3kmの地点でＡ君とすれちがったことに気付かず、Ａ君の家まで行って、Ａ君が留守だったので、すぐに自分の家に引き返しました。

　各自の家を出発した時刻は、Ｂ君のほうが１５分遅く、家に帰り着いた時刻は、Ａ君のほうが２５分遅かったとすると、v1、v2の速さはいくらになるでしょう。

２．解答例１(高橋道広さん、C-Dさん、他)

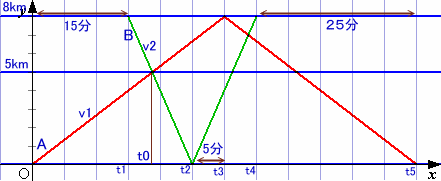
ダイアグラムで考えます。

参考図1

往復に要する時間差は、１５＋２５＝４０分ですから、片道では半分の２０分となります。
Ａ君は片道t3分、Ｂ君は（t2-t1）分かかるので、
　t3-(t2-t1)=20。
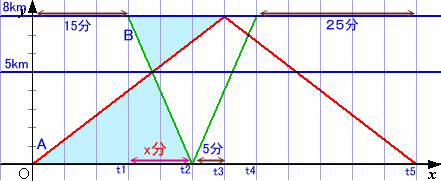
t1=15だから、t3-t2=20-15=5分となります。

x=t3-t2とおき、図の相似な三角形に着目すると、
　(x+5)：(x+15)=3：5
が成り立ちます。
よって、x+5=3k、x+15=5kとなるkがあります。

差をとると、
　(x+15)-(x+5)=5k-3k
　10=2k
よって、k=5、x=3k-5=10となります。

Ａ君は、片道８ｋｍを自転車でx+20=30分かかることなるので、
　v1=8/30×60=１６km/h
Ｂ君は、片道８ｋｍをバイクでx=10分かかることなるので、
　v2=8/10×60=４８km/h
となります。

答：１６km/h、４８km/h

以上

３．解答例２(ありっちさん、うっしーさん、noetherさん、あんみつさん、きょえぴさん、中村明海さん、DrKさん、大岡敏幸さん、はるみいさん、他多数)

ダイアグラムで考えるのは、解答例１と同じです。
Ａ君とＢ君が最初に出会う時刻をt0とします。

参考図2

連立方程式をたてます。 
往復に要する時間差から、
　16/v1 - 16/v2 = 40/60
よって、
　1/v1-1/v2=5/2/60 ・・・（１）

 最初に出会うまでの時間より、
　5/v1=15/60+3/v2
よって、
　5/v1-3/v2=15/60 ・・・（２）

ここで、60/v1=x1、60/v2=x2とおくと、
（１）、（２）は次のようになります。
　x1-x2=5/2　・・・（３）
　5x1-3x2=15　・・・（4）

（４）−（３）×３より、
　2x1=15/2、x1=15/4
よって、v1=4/15×60=１６km/h

（４）−（３）×５より、
　2x2=5/2、
よって、v1=4/5×60=４８km/h