第１５５問の解答

---

１．問題　［平面図形］

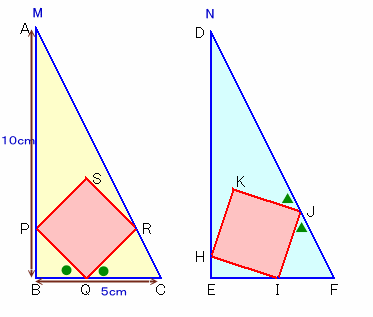
相似な２つの直角三角形ＭとＮがあります。 Ｍは底辺が５ｃｍ、高さが１０ｃｍと分かっていますが、Ｎのほうは分かりません。 そこで試しに同じ大きさの正方形のタイルを２枚用意して、タイルの頂点が直角三角形の各辺と接するように重ねたら、Ｍでは●の角度が等しくなり、Ｎでは△の角度が等しくなりました。 このとき、直角三角形Ｎの面積は、何ｃｍ2でしょうか。

---

２．解答例１(POIさん、うっしーさん、計算鑑定人さん、トトロ＠Ｎさん、高橋道広さん、他多数)

タイルの対角線を結びます。

図１

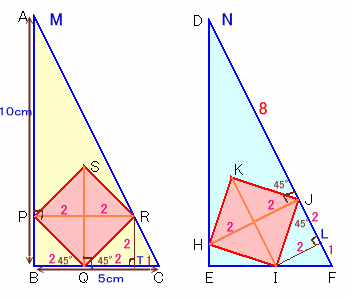
図２

●×２＋９０＝１８０°より、●＝４５°。
よって、ＱＳ⊥ＢＣ、ＰＲ⊥ＡＢ。

従って、△ＰＢＱ、△ＱＴＲは、いづれも正方形ＰＱＲＳの１／４。
また、△ＲＴＣ∽△ＡＢＣ。

よって、ＴＣの長さを１とすると、
ＲＴ＝２、ＢＱ＝ＱＴ＝２となり、ＢＣ＝２＋２＋１＝５となります。

従って、ＴＣ＝１ｃｍとなり、正方形の対角線の長さ＝ＢＴ＝４ｃｍとなります。

同様に、▲＝４５°となるので、ＨＪ⊥ＤＦ、IL⊥ＤＦ。
よって、ＪＬ＝２ｃｍ、ＬＦ＝１ｃｍとなります。

また、△ＤＪＨ∽△より、ＤＪ＝ＨＪ×２＝８ｃｍ。
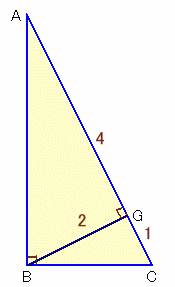
よって、ＤＦ＝８＋２＋１＝１１ｃｍと分かります。

図２のようにＢからＡＣに下ろした垂線の足をＧとし、ＣＧの長さを１とすると、
ＢＧ＝ＣＧ×２＝２、ＡＧ＝ＢＧ×２＝４。
よって、ＡＣ＝４＋１＝５。ＢＧ：ＡＣ＝２：５。

よって、
　三角形Ｎの面積
＝1/2×１１×（１１×２／５）
＝１２１／５
＝２４．２ｃｍ²となります。

答：２４．２ｃｍ²

以上

---

３．解答例２(貞松篤さん、パリンさん、みずなぎさん、BossFさん、他)

三角形Ｎの斜辺が１１ｃｍと分かったあと、下図のようにして面積（Ｓとおく）が求まります。

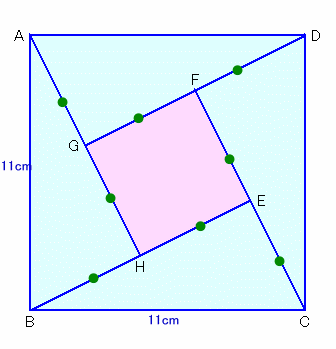
１辺１１ｃｍの正方形の中には、三角形Ｎが４個と、真ん中に１辺がＮの短辺の長さと等しい正方形が１個できます。

この正方形の面積もＳに等しいので、
　Ｓ＝１１²×1/5＝121/5＝２４．２ｃｍ²

　

---

４．解答例３(ありっちさん、他)

三角形Ｍの点Ｑから斜辺ＡＣに垂線ＱＴを下ろします。
これを逆方向に延長し、ＡＢの延長線との交点をＵとします。

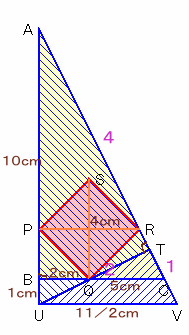
すると、△ＡＴＵ≡△ＡＢＣ。

解答例１と同様にして、正方形の対角線の長さＰＲ＝４ｃｍ、三角形Ｎの斜辺＝１１ｃｍがわかります。 

ＵからＢＣに平行に引いた直線とＡＣの延長との交点をＶとします。
△ＡＵＶ∽△ＡＢＣ∽△ＱＢＵ△ＵＴＶ。

ＢＱ＝２ｃｍより、ＢＵ＝１ｃｍ。
よって、ＡＵ＝１１ｃｍ、ＵＶ＝１１／２ｃｍとなります。

△ＵＴＶ：△ＡＴＵ＝１：４だから、
　△ＡＢＣ
＝△ＵＴＶ×４／５
＝1/2×１１×（１１／２）×４／５
＝１２１／５
＝２４．２ｃｍ² 

---

５．解答例４(ταροさん、他)

解答例１と同様にして、正方形の対角線の長さＰＲ＝４ｃｍ、三角形Ｎの斜辺＝１１ｃｍがわかります。 そこで、三角形Ｎで、正方形の対角線ＨＪの下に１辺が４ｃｍの正方形をくっつけます。

赤い２つの三角形は合同だから、正方形ＨＴＶＪが三角形Ｎよりはみ出ている部分の面積は正方形の半分＝４2／２＝８ｃｍ²。

緑の部分の三角形は三角形Ｎと相似で、斜辺の長さが１ｃｍなので、
面積はＳ/１１²。

よって、
Ｓ−Ｓ/１１²＝1/2×４×８＋８＝２４ｃｍ²。
Ｓ＝２４×１２１／１２０＝１２１／５＝２４．２ｃｍ²。

---