2.解答例1(ヒデー王子さん、たこやき大学さん、萬田銀次郎さん、うっしーさん、他多数)
求める整数をNとします。
N=7n+5=11m+4=13k+9と書けます。 ・・・ (1)3N=7・3n+7・2+1=11・3m+11+1=13・3k+13・2+1
従って、3N−1は7、11、13のいずれでも割り切れるので、
3N−1=7・11・13pと書けます。よって、最小の整数Nは、p=1のときで、
N=(7・11・13+1)/3=334となります。答:334
以上
3.解答例2(長野美光さん、Miki Sugimotoさん、あんみつさん、他多数)
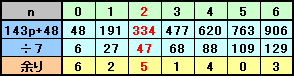
まず、N=7n+5=11m+4より、n=0、1、・・・、6について7n+5を計算し、これらから11で割った余りが4となるものを見つけます。
上の表より、n=3のとき、7・3+5=26、m=2のとき11・2+4=26となります。
従って、N−26=7・(n−3)=11・(m−2)となるので、
N−26は、7および11の倍数、すなわち77の倍数となります。
よって、N=77p+26と書けます。p=0、1、・・・、12について77p+26を計算し、これらから13で割った余りが9となるものを見つけます。
p=4のとき、N=77・4+26=13・25+9=334となります。
よって、求める整数の最小値は334と分かります。
(後半の別解)
77=13・6−1、26=13・2より、
N=77p+26=(13・6−1)p+13・2=13(6p+1)+13−p
よって、13−p=9、p=4となります。
4.解答例3(トトロ@Nさん、noetherさん、すうぱあさん、LIONさん、DrKさん、Taroさん、他多数)
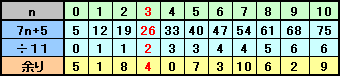
まず、N=11m+4=13k+9より、m=0、1、・・・、12について11m+4を計算し、これらから13で割った余りが9となるものを見つけます。

上の表より、m=4のとき、11・4+4=48、k=3のとき13・3+9=48となります。
従って、N−48=11・(m−4)=13・(k−3)となるので、
N−48は、11および13の倍数、すなわち143の倍数となります。
よって、N=143p+48と書けます。p=0、1、・・・、6について143p+48を計算し、これらから7で割った余りが5となるものを見つけます。
p=2のとき、N=143・2+48=7・47+5=334となります。
よって、求める整数の最小値は334と分かります。
(後半の別解)
143=7・20+3、48=7・6+6より、
N=143p+48=(7・20+3)p+7・6+6=7(20p+6)+3p+6
p=0、1、・・のとき、3p+6=6、9、12、・・。
7で割った余りは、6,2,5、・・。
よって、p=2、N=143+2+48=334となります。
5.解答例4(高橋道広さん、大岡敏幸さん、他)
N=7n+5=11m+4より、
11m−7n=1
4m+7(m−n)=1
4m+4n'+3n'=1 (n'=m−n)
4m'+3n'=1 (m'=m+n')
m'+3m'+3n'=1
m'+3n''=1 (n''=m'+n')
よって、m'=3t+1、n''=−tとなる。これより、
n'=n''−m'=(−t)−(3t+1)=−4t−1
m=m'−n'=3t+1−(−4t−1)=7t+2
n=m−n'=7t+2−(−4t−1)=11t+3
N=7・(11t+3)+5=77t+26となります。N=77t+26=13k+9より、
77t−13k=−17
(13・5+12)t−13k=−13−4
12t−13(k−5t−1)=−4
12t−13k'=−4 (k'=k−5t−1)
12t−12k'−k'=−4
12t'−k'=−4 (t'=t−k')
よって、k'=12s+4、t'=sとなります。これより、
t=t'+k'=s+12s+4=13s+4
k=k'+5t+1=(12s+4)+5・(13s+4)+1=77s+25
このとき、
n=11・(13s+4)+3=143s+47、
m=7・(13s+4)+2=91s+30。
よって、N=77・(13s+4)+26=1001s+334。
従って、Nの最小値は、s=0とおいて、N=334となります。
(参考)「中国剰余定理」
aで割るとp余る、bで割るとq余る、……、cで割るとr余 る自然数を求めるとき、
a、b、…、c が互いに素ならば、
(1) p、q、…、rの値に関わらず
(2) a×b× …×c以下の値であるもの
は、ただ1つ存在する。