2.解答例1(トトロ@Nさん、ヒデー王子さん、noetherさん、Miki Sugimotoさん、mhayashiさん、高橋道広さん、有無相生さん、他多数)
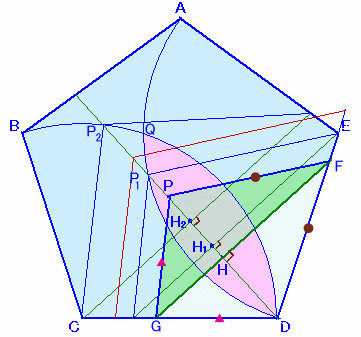
五角形の内部にある点Pへ、五角形の頂点Dを重ねるように折ったとき、折り返されて見える紙の裏側が三角形になるときを考えてみましょう。
そこで、Eが中心で、半径が五角形の1辺の長さrと等しい円を円E、
Cを中心とし、半径がrの円を円Cとします。折り返されて見える紙の裏側が三角形になる条件は、辺の折り目がDとEの間(これをFとする)、およびCとDの間(これをGとする)にあるときです。
さて、PF=DF、PG=DGですから、FGはPDの垂直二等分線になります。
直線DPと円Eの交点をP1、円Cとの交点をP2とします。△PFD∽△P1FDですから、
Pが円Eの内部にあるときは、DP≦DP1、従って、DF≦DE、
Pが円Eの外にあるときは、DP>DP1、従って、DF>DE。同様に、
△PGD∽△P2GDですから、
Pが円Cの内部にあるときは、DP≦DP2、従って、DG≦DC、
Pが円Cの外にあるときは、DP>DP2、従って、DG>DC。以上から、求める条件は、点Pが円Cと円Eの共通部分の中ににあることとなります。
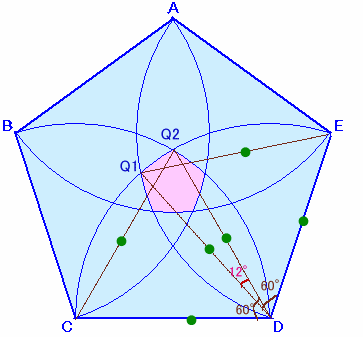
他の頂点についても同様ですから、結局点Pは、円A、円B、円C、円D、および円Eの共通部分内(正五角形が丸っこくなった赤い部分)にあることになります。
円Dと円Eの交点をQ1、円Dと円Cの交点をQ2とします。
EQ1=DQ1=DE=r、CQ2=DQ2=CD=rより、
△EQ1D、△CQ2Dはともに正三角形となります。∠CDEは正五角形の内角だから、180−360/5=108度。
よって、
∠Q1DQ2=∠EDQ1+∠CDQ2−∠CDE
=60+60−108
=12度。従って、円弧Q1Q2=2πr×12/360。
よって、求める長さLはこの5倍だから、
L=5×2πr×12/360
=2π×5×6×12/360
=2π
≒6.28cmとなります。答:6.28cm
以上