第１５９問の解答

１．問題　［整数の性質］

10/11よりも大きく11/12よりも小さい分数の中で、
分子が最も小さい分数は、何分の何でしょうか？
　

２．解答例１(Miki Sugimotoさん、ありっちさん、たこやき大学さん、トトロ＠Ｎさん、萬田銀次郎さん、すうぱあさん、Taroさん、清川育男さん、DrKさん、中学への算数学コンさん、他多数)

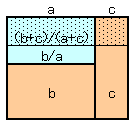
次の補題を用います。（ただし、数は全て正）

（補題１）c<b<aのとき、b/a<(b+c)/(a+c)
　　b(a-c)-a(b-c)
　　＝ac-bc
　　＝(a-b)c>０
よって、
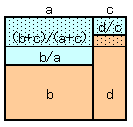
　　(b-c)/(a-c)<b/a		 参考図1
（補題２）a<c、b<d、b/a<d/cのとき、b/a<(b+d)/(a+c)<d/c
　b/a<d/cより、ad-bc>0
　　a(b+d)-b(a+c)
　＝ad-bc>０
よって、
　b(a+c)<a(b+d)
　b/a<(b+c)/(a+c)		 b/a<d/cより、ad-bc>0
　d(a+c)-c(b+d)
　＝ad-bc>０
よって、
　c(b+d)<d(a+c)
　(b+d)/(a+c)<d/c		 参考図2

　a=11、b=10、c=1とおくと、
補題１より、
　20/22<(20+1)<(22+1)=21/23
　a=12、b=11、c=1とおくと、
補題１より、
　21/23<(21+1)/(23+1)=22/24
よって、20/22<21/23<22/24、
　10/11<21/23<11/12。

　a=11、b=10、c=12、d=11とおくと、
補題２より、
　10/11<(10+11)/(11+12)<11/12、
　10/11<21/23<11/12。　 

　答：２１／２３

以上

３．解答例２(Taroさん、Miki Sugimotoさん、他)

一般化して、(m-1)/mより大きくm/(m+1)より小さい分数q/pを求めます。

　(m-1)/m<q/p<m/(m+1)
　1-1/m<1-q'/p<1-1/(m+1)　（q'=p-qとおきます）
　1/(m+1)<q'/p<1/m
　q'/(q'm+q')<q'/p<q'/q'm
よって、q'm<p<q'm+q'。

q'=1とすると、m<p<m+1となり不適。

q'=2とすると、2m<p<2m+2となり、p=2m+1、q=p-q'=2m-1。

q'>2とすると、p=q'm+r（ただし、1≦r≦q'-1）、
　q=p-q'=q'm+r-q'≧q'm+1-q'=q'(m-1)+r>2(m-1)+1=2m-1。

従って、q=2m-1が最小。

よって、q/p=(2m-1)/(2m+1)となります。

本問では、m=11なので、q/p=(2・11-1)/(2・11+1)=21/23となります。