|
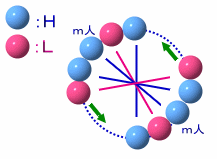
いつも嘘をついてしまう嘘つき者と、絶対に嘘をつかない正直者が何人かずつ集まったグループがあります。このグループ全員に、円形に等間隔に並んでもらい、それぞれ円の中心方向に向いて立ってもらいました。
この状態でみんなに「あなたの右隣の人は嘘つきですか?」と尋ねたところ、 また、同じ並びのままで、「あなたの真正面に立っている人は、嘘つきですか?」と尋ねたところ、 では、このグループの人数は少なくとも何人いると考えられるでしょうか? |
2.解答例1(ありっちさん、Taroさん、トトロ@Nさん、萬田銀次郎さん、ちーくん、C-Dさん、ふぇるまーさん、Miki Sugimotoさん、高橋道広さん、すうぱあさん、澪桜葵美翔さん、あやのりんさん、小杉原啓さん、あんみつさん、みずなぎさん、有無相生さん、他多数)
正直者をH、嘘つき者をLとおきます。
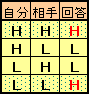
自分と訊かれた相手の組み合わせで、回答がどうなるかは下表のとおりです。
まず、全員とも向かい合わせの人間がいるということは、全員の人数は偶数です。2m人とします。
また、上表からその相手は自分と同じグループ(HHまたはLL)に属します。
従って、全体としては、m人ずつの同じパターンからなる2つのグループに分かれることになります。
もし、mが奇数だと、m人の回答はHとLが同数になることありませんから、全体はこの2倍ですから、HとLは同数ではなく、不適です。
よって、mは偶数となります。
また、これらm人のグループはHのみ、あるいはLのみとなることはありません。もしそうだとすると、回答が全てHになるので不適だからです。
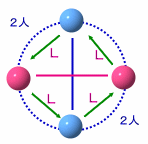
よって、H、Lが一人は存在します。さて、m=2とします。
H、Lともに一人は存在することから、2人のパターンは、HLでなければなりません。ところが、このとき2人の回答は、LLとなり不適。
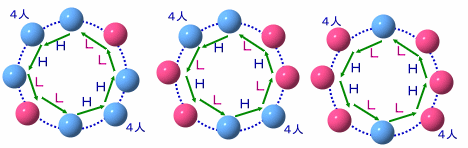
m=4とします。
4人のパターンは、HHHL、HHLL、HLHL、HLLLの4通り考えられます。
それぞれ回答は、HHLL、HLHL、LLLL、LHHHとなるので、3番目のパターン以外は題意に適します。
よって、全体の人数は、最小で2m=8人いることになります。
答:8人
以上