第１６３問の解答

１．問題　［推理］

Ａ君とＢさんが、次のようなルールでじゃんけんの５回勝負を行いました。
  • ぐうで勝った場合：＋１ポイント、　ぐうで負けた場合：−１ポイント
  • ちょきで勝った場合：＋２ポイント、ちょきで負けた場合：−２ポイント
  • ぱあで勝った場合：＋３ポイント、　ぱあで負けた場合：−３ポイント

この結果、Ａ君の最終ポイントは＋４、Ｂさんは−６だったそうです。
２人ともぐう、ちょき、ぱあを少なくとも１回は出したとすると、２人が出したぐう、ちょき、ぱあのそれぞれ何回だしたでしょうか？

２．解答例１(まるケンさん、トトロ＠Ｎさん、他)

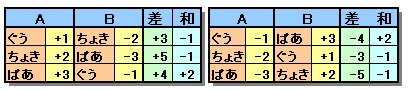
Ａ、Ｂが出す手によって決まるポイントの組み合わせは下表のとおりです。

参考図1

各勝負でつくポイント差に注目して考えます。

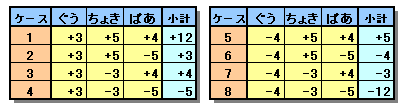
Ａは、ぐう、ちょき、ぱあを少なくとも１回ずつ出し、そのとき勝ったか負けたかによって下表のように８通りのケースがあります。

参考図2

最終的なポイント差は+10ですが、 残り２回の勝負で生じるポイント差は、-10〜-6、-2〜+2、+6〜+10の範囲となるので、ケース４〜ケース８は題意に適しません。

（ケース１）　
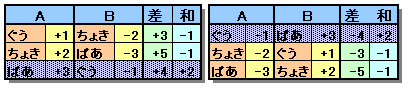
　残り２回でポイント差が-2となるのは、+3、-5となるとき。
　従って、５回の勝負は+3、+3、+4、+5、-5。
　　Ａのポイントは、+1、+1、+3、+2、-3、合計+4、
　　Ｂのポイントは、-2、-2、-1、-3、+2、合計-6
　となる。

　また、このとき、
　　Ａの手は、ぐう２回、ちょき１回、ぱあ２回、
　　Ｂの手は、ぐう１回、ちょき３回、ぱあ１回、
　となるので題意に適する。

（ケース２）　
　残り２回でポイント差が+7となるのは、+3、+4となるとき。
　従って、５回の勝負は+3、+3、+4、+5、-5。これは、ケース１と全く同じ。

（ケース３）　
　残り２回でポイント差が+6となるのは、+3、+3となるとき。
　従って、５回の勝負は+3、+3、+3、+4、-3。
　　Ａのポイントは、+1、+1、+1、+3、-2、合計+4、
　　Ｂのポイントは、-2、-2、-2、-1、+1、合計-6
　となるが、
　　Ａの手は、ぐう１回、ちょき３回、ぱあ１回、
　　Ｂの手は、ぐう０回、ちょき４回、ぱあ１回
　となるので題意に不適。

答：Ａ：ぐう２回、ちょき１回、ぱあ２回、Ｂ：ぐう１回、ちょき３回、ぱあ１回

以上

３．解答例２(長野美光さん、Taroさん、中村明海さん、川田智之さん、他)

両者のポイント和に着目すると、ぱーで勝ったときのみ、両者の得点和が+2で、他は-1なので、５回中１回がぱーで勝ち、他４回がぐーかちょきで勝ちとなります。

実際、ぐうで勝ったのをｘ回とすると、
　２ｘ−（５−ｘ）＝−２
　３ｘ＝３
よって、ｘ＝１となります。

参考図3

ぱーで勝ったのがＢとすると、ポイント差は-4。
Ａはぱあを少なくとも１回は出したが、これは負けのケースでポイント差は-5、
従ってこの２回でポイント差が-9となり、残りの３回でポイント差+19にはなりえないので不適。

従って、ぱーで勝ったのがＡであり、ポイント差は+4、このときＢはぐう。

次に、Ａは少なくともぐうを１回出したが、このときＢの手はちょきでＡの勝ち、ポイント差は+3。

さらに、Ｂはぱあを少なくとも１回出したが、このときＡの手はちょきでＡの勝ち、ポイント差は+5。

ここまでの３回で、Ａ、Ｂともぐう、ちょき、ぱあをそれぞれ１回ずつ出したことになり、ポイント差は合計+12。

これは解答例１のケース１の場合であり、以下省略。