第164問の解答
1.問題 [平面図形]
 |
|
第164問の解答
1.問題 [平面図形]
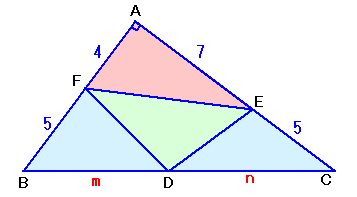
左図の△ABCはAB:AC:BC=3:4:5の直角三角形です。 AF:BF=4:5、AE:CE=7:5となるよう点F、Eをとり、辺BC上に点Dをとったところ、△AEF=△DEFとなりました。
このとき、BD:CDは何:何でしょうか?
2.解答例1(YokoyaMacさん、POIさん、あやのりんさん、Taroさん、計算鑑定人さん、トトロ@Nさん、他多数)
AB=9cm、AC=12cm、BC=15cmとして考えます。
点DがちょうどBおよびCに重なった場合の面積を計算してみましょう。
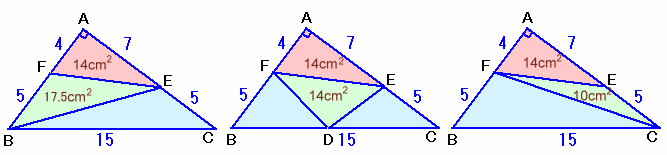
点DがBに重なったとき:
△FDE=△FBE=△ABE×7/12=△ABC×5/9×7/12
=54×5/9×7/12=35/2=17.5cm2。点DがCに重なったとき:
△FDE=△FCE=△AFC×5/12=△ABC×4/9×5/12
=54×4/9×5/12=10cm2。さて、点DがCからBへ動かしていくとき、△FDEの面積は、底辺FEが共通だから高さに比例、すなわちDCの長さに比例して増えていきます。
15cm増えたところで、面積の増加分は17.5−10=7.5cm2。
従って、4cm2増えて△AFEと等しい14cm2になるのは、
DC=15×4/7.5=8cmのとき、よってBD:DC=7:8のときです。答:7:8
以上
3.解答例2(数楽者さん、Taroさん、げんさん、他)
AB=9cm、AC=12cm、BC=15cmとして考えます。
点B、A、D、Cからそれぞれ直線FEに下ろした垂線の足をG、H、I、Jとします。
AHの長さを28とすると、
△BFGと△AFHが相似より、BG=AH×5/4=35、
△CEJと△AEHが相似より、CJ=AH×5/12=20
となります。
また、△DFE=△AFEだからDI=AH=28となります。ここで、点Cを通って直線FEに平行な直線を引き、BG、DIとの交点をK、Mとします。
BK=BG−KG=35−20=15、
DM=DI−MI=28−10=8。△CKBと△CMDは相似だから、DC:BC=MD:KB=8:15、
よって、BD:DC=7:8となります。
4.解答例3(たなかさん、他)
点Dを通りEFに平行線を引き、直線ACおよびABとの交点をI、Jとします。
△AFE=△FDEより、GH=KD=AG、
従って、F、EはAJ、AIの中点となり、FJ=4、JB=1、CI=2となります。△ABCおよび直線JIに関してメネラウスの定理より、
(AJ/JB)・(BD/DC)・(CI/IA)=1
(8/1)・(BD/DC)・(2/14)=1
よって、BD:DC=7:8となります。
5.解答例4(長野美光さん、中村明海さん、高橋道広さん、他)
点Dを通り EFに平行線を引き、直線ACおよびABとの交点をG、Hとします。
また、Bを通りACに平行に引いた直線とGHの延長線との交点をIとします。
解答例3と同様にして、FH=4、HB=1、CG=2となります。
△AFE=△FDEより、点Dは直線GI上になければなりません。
従って、DはGIとBCの交点に他なりません。△BHIと△AFEは相似より、BI=HB×AF/AE=7/4。
△DBIと△DCGは相似より、BD:DC=BI:CG=(7/4):2=7:8となります。
(その他の解法)
面積等より、方程式を解く
・・・Gouさん、あんみつさん、うっしーさん、noetherさん、ちーくん、
杉本未来さん、C-Dさん、圭太さん座標で考え方程式を解く・・・高橋道広さん、ありっちさん、有無相生さん