第１６５問の解答

１．問題　［場合の数］

Ａ〜Ｅの５チームが参加して、サッカーの総当たり戦を行うことになりました。
全１０試合を毎日１試合ずつ１０日間に分けて行います。１日目の対戦カードは、前回優勝のＡチームvs初参加のＥチームと決まりました。

組織委員会は残り９試合の対戦順を考えています。どのチームも、試合をした翌日は試合がないように対戦カードの順番を決めるとき、

  1. これらの決め方の中で、最終日の試合にＡチームが出場するような決め方は何通り考えられますか？
  2. 全部で何通りの決め方があるでしょう？

２．解答例１(トトロ＠Ｎさん、杉本未来さん、Taroさん、Gouさん、高田修成さん、長野美光さん、高橋道広さん、あんみつさん、有無相生さん、圭太さん、他多数)

Ａチームがいつ対戦するかに注目して考えます。
ＡチームがＥチーム以降に対戦する順番を選ぶ選び方は、Ｂ、Ｃ、Ｄを並べる順列の数＝３！＝３×２×１＝６通りありますので、Ｂ、Ｃ、Ｄの順番に対戦する場合を数えれば、その６倍が全体の場合の数となります。

参考図1

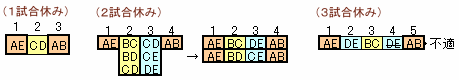
Ａチームが対戦の間に休む試合数に場合分けしてみましょう。
（１）１試合休む場合

途中の対戦カードは１通り（上記例では、Ｃ対D）に決まります。

（２）２試合休む場合

途中の対戦カードは２通りになります。
（上記例では、B対Ｃ、Ｄ対ＥまたはＢ対Ｄ、Ｃ対Ｅ）

なぜなら、２試合目はＡ、Ｅチームとも休みですから、Ｂ、Ｃ、Ｄの３チームが対戦する３通り、３試合目はＣ、Ｄ、Ｅチームの対戦３通りありますが、２試合目が決まれば３試合目は自動的に決まり、２試合目がＣ対Ｄのときは不適だからです。

（３）３試合以上休む場合

不適となります。

なぜなら、例えば上記例で３試合目がＢ対Ｃとすると、２試合目も４試合目も（１）の場合同様１通り（同じ対戦）になってしまうからです。

次に、Ａチームが何試合目に対戦するかを考えてみましょう。
上記より、
［１、４、７、１０］、［１、４、７、９］、［１、４、６、９］、［１、４、６、８］、
［１、３、６、　９］、［１、３、６、８］、［１、３、５、７］
の７ケースに限られることが分かります。

Ｅチームの対戦も同様ですが、Ａ対Ｅのカードは第１試合のみですから、それ以降同じ試合に登場することはありません。

（１）Ａチームが第４試合に出るとき

  1. Ａ：［１、４、７、１０］　　Ｅ：［１、３、６、９］

  2. Ａ：［１、４、７、１０］　　Ｅ：［１、３、６、８］

  3. Ａ：［１、４、７、　９］　　Ｅ：［１、３、６、８］

  4. Ａ：［１、４、６、　９］　　Ｅ：［１、３、５、７］

  5. Ａ：［１、４、６、　８］　　Ｅ：［１、３、５、７］

（２）Ａチームが第３試合に出るとき

  1. Ａ：［１、３、６、　９］　　Ｅ：［１、４、７、１０］

  2. Ａ：［１、３、６、　８］　　Ｅ：［１、４、７、１０］

  3. Ａ：［１、３、６、　８］　　Ｅ：［１、４、７、　９］

  4. Ａ：［１、３、５、　７］　　Ｅ：［１、４、６、　９］

  5. Ａ：［１、３、５、　７］　　Ｅ：［１、４、６、　８］

の１０ケースに限られます。
ところが、（１）と（２）は、ＡチームとＥチームを入れ替えた場合に相当しますので、（１）のみを考えれば十分です。

（１）−１、２の場合

参考図2

途中の試合は、それぞれ２通りありますが、第５試合にＥチームが出ることはありません。結局、題意に適するのは、２通りあることが分かります。

（１）−３、４、５の場合

参考図3

Ｅチームの試合順に不適なものをまず除くと、
　（１）−３の場合は、第６、８試合に同じＢ対Ｅが来て不適
　（１）−４の場合は、第８、１０試合に同じＢ対Ｃが来て不適
　（１）−５の場合は、この時点で不適
となり、いずれの場合も不適となります。

（２）の場合は、以上から（２）−１、２のみ適することが分かります。
実際、（１）−１、２でＡとＥを入れ替え、さらにＡチームの対戦相手がＢ、Ｃ、Ｄの順になるように入れ替えすると、下図のように２通りの結果が得られます。

参考図4

以上より、最後の試合にＡチームが出るのは、（１）−１、２の２通り×６＝１２通り、出ないのは、（２）−１、２の２通り×６＝１２通り、合計２４通りとなります。　

答：（１）１２通り（２）２４通り

以上

３．解答例２(電子滅入さん、数楽者さん、他)

１０の対戦カードを円で表し、その前後に選べる対戦カード同士を線分で結んで考えます。解答例１で見たように、１つの対戦カードと結べるカードは３個となりますので、全体として下図のように表せます。

参考図5

解答例１と同様、Ａチームが出るカードに着目し、対戦相手はＢ、Ｃ、Ｄの順として考えます。

（１）最後の試合にＡチームが出る場合

解答例１で第１、４、７、１０試合に出るケースしかないので、下記の２通りになることが容易に分かります。

参考図6

（２）最後の試合にＡチームが出ない場合

下記の２通りになることが分かります。

参考図7

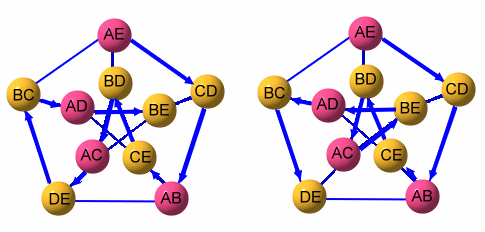
従って、最後の試合にＡチームが出るのは、２×６＝１２通り、全体では４×６＝２４通りとなります。