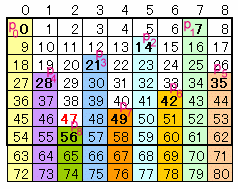
第166問の解答
1.問題 [整数の性質]
初詣に近所の神社に出かけたゆたか君は、ちょっと変わった21世紀記念おみくじを引くことになりました。そのおみくじとは、次のようなものです。 箱の中に、金、赤、青、白の小さな玉がそれぞれ沢山入っていて、ここから玉を1個ずつ金色の玉が出るまで取り出し続けます。
赤を取り出すと93点、青が出たら56点、白が出たら37点が順次加点され、金が出たら21点を加えて玉を取り出す作業は終了し、総得点を計算します。
また、壁には得点の総計が書かれているボックスが並んでいて、総得点に該当するボックスの中から1枚おみくじを取り出して渡してくれます。さて、壁には得点の可能性がある21点や58点のボックス、・・・などがずらーーっと並んでいるのですが、得点する可能性のない数字を書いたボックスは、はじめから用意されていません。
従って、ある数字までは、数字がまばらになっているのですが、このある数字を書いたボックスが用意されていないのを最後に、その後は全ての数字のボックスが並べられていました。では、このある数字とはいったい何なのでしょうか?
2.解答例1(AUさん、Michaelさん、Taroさん、長野美光さん、萬田銀次郎さん、中村明海さん、高橋道広さん、ミミズクはくず耳さん、DrKさん、圭太さん、数楽者さん、他多数)
93=56+37なので、赤が1個出ることは、青、白1個ずつ出ることと同等になりますので、赤色の玉は無視して構いません。
また、金色の玉は最後に1個だけ出るので、結局、
(青色の玉の個数)×56+(赤色の玉の個数)×37で表せない整数で最大のものを求め、それに21を加えれば良いことになります。(補題1)
pとqが互いに素な正の整数のとき、np+mq(n,m≧0)で表せない整数の最大値は、pq-(p+q)である。p=56、q=37とすれば補題より、求める数は56×37-(56+37)+21=2000となります。
(補題1の証明)
横q列の表に整数を0から順に並べていき、その中からpの倍数に印をつけます。 (下表は、p=7、q=9のとき)
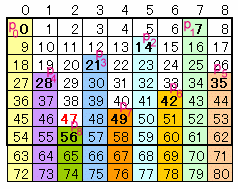
Pn={np、np+q、np+2q、np+3q、・・}とすると、Pnの各数は、np+mqで表されており、表では、npと同じ列で、npより下に順番に並んでいます。
ところが、p0からpq-1は、qで割った余りが全て異なる(補題2)ので、np+mqで表される整数は、P0、P1、・・、Pq-1のいずれかに入っていることになります。
従って、np+mpでは表せない整数の最大値は、Pq-1の1段上の整数、すなわち(q-1)p-q=pq-(p+q)となります。(補題2の証明)
もしpnとpmがqで割った余りが等しいと仮定します。
(ただし、0≦n<m≦q-1)すると、mp-np=(m-n)pがqの倍数になりますが、これは0<m-n<q、およびpとqは互いに素ということに反します。
従って、補題2が成り立ちます。
答:2000
以上