第１６７問の解答

---

１．問題　［整数の性質］

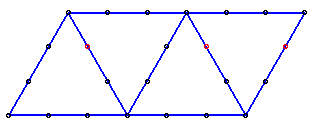
左図は、正四面体の展開図と、その各辺を３等分する点を表したものです。 まず、これを組み立て、赤色の３点を通る平面で四面体を切断したところ、切り口の面積が４cm2ありました。 では組み立ててできた四面体の体積は何cm3あったでしょうか？

---

２．解答例１(Taroさん、うっしーさん、ミミズクはくず耳さん、大岡敏幸さん、圭太さん、kakeruさん、他多数)

展開図で各点に名前を付け、組み立てます。
正三角形の１辺の長さをａとします。

ＰとＲ、ＲとＱは同じ面にありますが、ＰとＱは同じ面にはありません。
ここで、点Ｂ、Ｃを１：２に内分する点をＳとすると、四角形ＰＳＱＲが切り口となります。

△ＡＰＲ∽△ＡＣＤで相似比は１：３。よって、ＰＲ＝1/3×ａ。
△ＢＳＱ∽△ＢＣＤで相似比は１：３。よって、ＳＱ＝1/3×ａ。

△ＣＡＢ∽△ＣＰＳで相似比は２：３。よって、ＰＳ＝2/3×ａ。
△ＤＡＢ∽△ＤＲＱで相似比は２：３。よって、ＲＱ＝2/3×ａ。
よって、ＰＳ＝ＲＱ＝2/3×ａ。
これから、四角形ＰＳＱＲは平行四辺形となります。

そして、Ａ、Ｂ、およびＣＤの中点を通る平面を軸にして、ＰとＲ、ＳとＱが対称であることから、四角形ＰＳＱＲは長方形と分かります。

ＰＲ＝ｂとおくと、長方形ＰＳＱＲの面積＝ｂ×２ｂ＝４cm²、
よって、ｂ＝√２ｃｍ。ａ＝３√２ｃｍ。

よって、正四面体の体積Ｖは、
　Ｖ＝√２/１２×ａ³＝√２/１２×２７×２√２＝９ｃｍ³
となります。

答：９ｃｍ³

以上

---

３．解答例２(C-Dさん、長野美光さん、高田修成さん、萬田銀次郎さん、Taroさん、高橋道広さん、他多数)

切り口が長方形であることまでは、解答例１と同じ。
正四面体がすっぽり収まる立方体（１辺の長さｄ）を考えます。

解答例１より、１辺の長さがｂの正方形の面積が２ｃｍ²より、
対角線の長さｃ＝２ｃｍ。

ｄ：ｃ＝ＢＤ：ＱＤ＝３：２より、ｄ＝３ｃｍ。
従って、立方体の体積はｄ³＝２７ｃｍ³。

正四面体の体積は、立方体の３分の１（注１）＝２７ｃｍ³×1/3＝９ｃｍ³。

（注１）正四面体は、立方体より三角錐４個を除いたものとなるので、
　　　　体積Ｖ＝ｄ³−（1/3×1/2×ｄ²×ｄ）×４＝1/3×ｄ³

---