第１７０問の解答

１．問題　［場合の数］

問題図

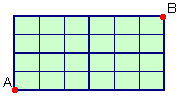
左図のように２地点Ａ、Ｂの間には太い道路と細い道路が通っています。
ＡからＢまで遠回りをせずに行くとき、細い道路から太い道路にでた場合にはそのまま直進できず、必ず太い道路に曲がらなければなりません。

では、このような道順は何通りあるでしょうか？

２．解答例１(杉本未来さん、長野美光さん、圭太さん、NobleScarletさん、他多数)

下図のように、Ａ地点を１とし、各格子点を通る場合の数を順に加えていきます。

参考図1

ただし、細い道路から太い道路へ出た場合、直進するものは数えないようにします（赤い格子点）。この結果、Ｂ地点に至る経路数は１２６通りになります。

答：１２６通り

以上

３．解答例２(トトロ＠Ｎさん、あんみつさん、noetherさん、有無相生さん、mhayashiさん、King of Kingさん、N.Nishiさん、他多数)

n×m個のマス目上の最短経路数は、一般にn+mCn＝(n+m)!/n!m!で表せます。従って、ＡからＢへ至る最短経路の合計は6+4C6＝２１０通りあります。

このうち、細い道路から太い道路に出たとき直進する場合は下図のように６ケースあります。

参考図2

それぞれの経路数は、次の通り合計１１４通りあります。

参考図3

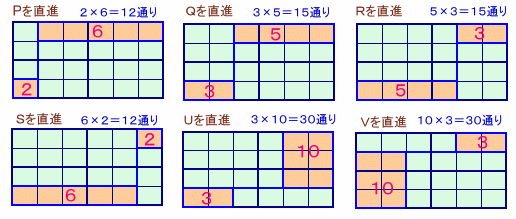
ところが、これには下図のように重複して数えたものが３０通りあるので、これを除外する必要があります。 

参考図4

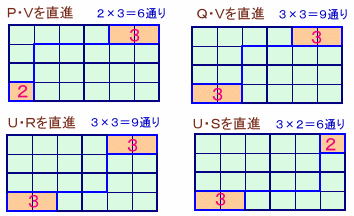
従って、求める経路数は、２１０−（１１４−３０）＝１２６通りとなります。