第１７３問の解答

---

１．問題　［推理］

Ａ君とＢ君が次のようなルールのカードゲームをしています。 各自が最初、２０のポイントを２枚のカードに振り分けます。 お互いが、２枚のうちのどちらかのカードを１枚選んで出します。 相手が出したカードの数値の半分だけ、自分が出したカードのポイントを減らします。 ただし、ポイントは０より小さくなることはしません。 残りポイントの大きい方が勝ちとなり、勝ったほうは、２枚のカードの残りポイントの和をポイントとする新たなカードを手に入れ、負けたほうはカードを失います。 何回か対戦を続け、手持ちのカードが無くなったら負けです。 さて、Ａ君は最初に２０ポイントを、１５と５に分けました。Ｂ君も振り分け終わって、どちらのカードを出そうか作戦を考えています。 Ｂ君：「君が１５と５に振り分けたとすると、どうやら僕が勝てそうだ。ただし、カードを出す順番を間違えると負ける可能性もある。」 では、Ｂ君が最初に振り分けた２つの整数は？大きい方の数で答えてください。

---

２．解答例１(sodoさん、小杉原啓さん、きょえぴさん、高橋道広さん、CRYING DOLPHINさん、中村明海さん、圭太さん、N.Nishiさん、とらいしくるさん、他多数)

A君はaとc(a≧c、a+c=20)、Ｂ君はbとd(b≧d、b+d=20)に振り分けるとします。
　(ただし、b>a=10)

　

（１）Ｂ君に必勝法があること

b>a,cなので、Ｂ君は、最初にbのカードを出せば必ず勝ちます。
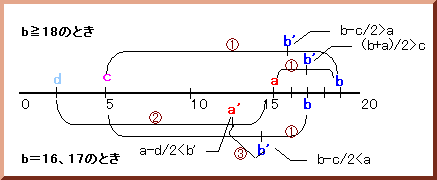
新しく得るカードの数b'は、

• A君がaを出したとき・・・a-b/2>15-20/2>0だから、
  b'=(b+a)/2>a>c

• A君がcを出したとき・・・c-b/2<5-10/2=0だから、
  b'=b-c/2　となります。

もしb≧18なら、b'=b-c/2=b-2.5>a=15となるので、次にB君はb'を出せば必ず勝ち、ここで勝負が決まります。

もしb=17、18なら、b'=b-c/2=b-2.5<a=15となるので、
最初にＡ君がaを出したときは、次にB君はb'を出せばＡ君の出すcより大きいので必ず勝ち、勝負あり。

ところが、最初にＡ君がcを出したときは、次にB君はb'を出してもＡ君の出すaより小さいので負けます。

そこで、２度目はb'でなくdを出すことにします。
すると、この回はＡ君が勝ち、新たにa'=a-d/2を得ます。

三度目の勝負は、Ａ君が最後に残ったa'、Ｂ君がb'を出します。
　b'-a'=(b-c/2)-(a-d/2)=(b-a)-(c-d)/2
　　　　=(b-a)-(b-a)/2=(b-a)/2>0
よって、Ｂ君の勝ちとなります。

（２）b=16、17のとき、Ｂ君は下手をすると負ける可能性があること

最初は、Ａ君がc、Ｂ君がbを出し、B君の勝ち、b'=b-c/2とします。

次に、A君が残ったa、B君は続いてb'を出したとします。
Ａ君の勝ちで、a'=(a+b')/2>a/2>dとなるので、
最後の勝負では、Ｂ君の出すdはＡ君のa'に勝てません。

（３）b≧18のとき、Ｂ君はどんな手順でカードを出しても必ず勝つこと。

• Ｂ君が最初bを出す場合
  Ａ君がa,cどちらを出してもＢ君の勝ち。
  （ア）２度目はＢ君はb'を出せば、Ｂ君の連勝で勝負あり。
  
  （イ）２度目にＢ君がdを出したとき、この回はＢ君の負け。
  　Ａ君が得るカードは、
  　(i)最初Ａ君がaを出したとき、c'=c-d/2またはc'=(c+d)/2
  　(ii)最初Ａ君がcを出したとき、a'=a-d/2
  
  最後の勝負は、Ａ君はa'またはc'、B君はb'です。
  ところが、b>a>a'、b>c>c'なので、B君の勝ちで勝負あり。
  

• B君が最初dを出す場合
  Ａ君がa,cどちらを出してもA君の勝ちで、a'またはc'を新たに得ます。
  
  Ａ君の持つ２枚のカードは、最初の状態よりもいずれかは小さくなっています。従って、Ｂ君は残ったbのカードで連勝可能です。
  

以上より、手順良く出せば必勝だが、手順を間違えると負ける可能性があるのは、b=16、17のときと分かります。

答：１６または１７

以上