第１７５問の解答

１．問題　［平面図形］

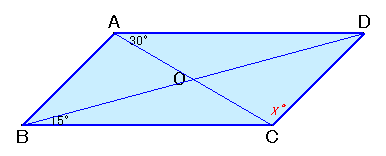
左図のABCDは、平行四辺形で、∠DAC=３０度、∠DBC=１５度です。
では、∠ＡＣＤは何度でしょうか？

　

２．解答例１(トトロ＠Ｎさん、うっしーさん、他多数)

ＡからＢＣに下ろした垂線の足をＨ、ＯからＢＣに下ろした垂線の足をＥ、ＡＤに下ろした垂線の足をＦとします。

　図1

△ＯＥＨ、△ＯＥＣ、△ＯＦＡは合同な直角三角形。
よって、ＯＥ＝１とすると、ＡＨ＝ＥＦ＝２×ＯＥ＝２、
また、∠ＯＨＥ＝３０度より、ＯＨ＝２×ＯＥ＝２。

∠ＢＯＨ＝∠ＯＨＥ−∠ＯＢＨ＝３０−１５＝１５度、
よって、△ＨＯＢは二等辺三角形、ＢＨ＝ＯＨ＝２。

従って、△ＡＢＨは直角二等辺三角形となり、∠ＡＢＨ＝４５度。

よって、∠ＢＣＤ＝１８０−∠ＡＢＨ＝１８０−４５＝１３５度。
∠ＡＣＤ＝∠ＢＣＤ−∠ＡＣＢ＝１３５−３０＝１０５度。

答：１０５度

以上

（その他の解法）

三角関数で求める・・・有無相生さん、他