第１７６問の解答

１．問題　［その他（仕事算）]

全く同じ円筒形の容器を２個用意し、一方には水道管Aで、もう一方には水道管Ｂで、同時に水を入れ始めました。
水道管Ａは水を入れている間に１度だけ数分間の断水がありました。
上図は、水を入れ始めてからの時間と、双方の容器に入った水の深さの差を表したグラフです。

では、使用した容器の深さは何ｃｍでしょうか？

２．解答例１(ミミズクはくず耳さん、Gouさん、小杉原啓さん、Ｈｉｒｏさん、トトロ＠Ｎさん、れえさあ♪さん、パリンさん、長野美光さん、noetherさん、Ｍｉｙａ−Ｎさん、うっしーさん、DrKさん、大岡敏幸さん、他多数)

題意より、経過時間と水の深さを図で表すと、図１および図２のようになります。

図１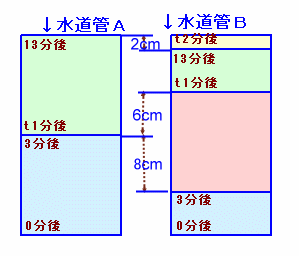
図1		 図２
図2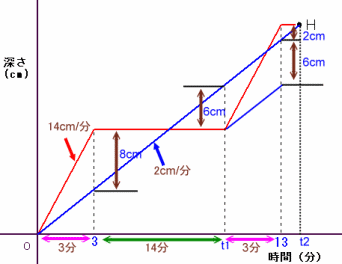

水道管Ａが断水した時間の始まりは３分後で、終わりをt1分後とします。
１３分後にはＡのほうの容器は一杯になり、またＢ側の容器が一杯になるのをｔ２分後とします。

ｔ１〜１３分後の間に、Ａ側から見た水の深さの差は、−６〜２ｃｍの８ｃｍ増えることになります。

これは、ちょうど最初の０〜３分後の８ｃｍと同じなので（１３−ｔ１）＝３、
従って、ｔ１＝１０分後と分かります。

すると、断水したのは３〜１０の７分間となり、この間Ｂ側だけ水が入り、８＋６＝１４ｃｍだけ深さが増します。

従って、Ｂの深さが増す割合は、１４ｃｍ／７分＝２ｃｍ/分の割合となります。

よって、Ｂは０〜１３分後までに１３×２＝２６ｃｍ深さが増し、１３〜ｔ２に２ｃｍ増すので、容器の深さは２６＋２＝２８ｃｍと分かります。　

また、Ａは０〜３分の間に、Ｂが増える３×２＝６ｃｍとＡ、Ｂの差８ｃｍの合計１４ｃｍ増えることになり、１０〜１３分の３分間でも同じ１４ｃｍ、
従って、合計では１４＋１４＝２８ｃｍ、これが容器の深さとなり、先ほどの結果と合致します。

答：２８cm

以上

（その他の解法）

・真ん中の谷を反対方向に折り返した図で考える　・・・　
　　ＫＩＮさん、高橋道広さん、ちーくん、kakeruさん、他

図3

・図２のダイアグラムで相似な三角形３個、相似比８：６：２から求める　・・・　
　　中村明海さん、CRYING DOLPHINさん、N.Nishiさん、BossFさん、他

・ダイヤグラムから連立方程式をたてて、これを解く　・・・　AUさん、他