第１７８問の解答

１．問題　［平面図形]

問題図
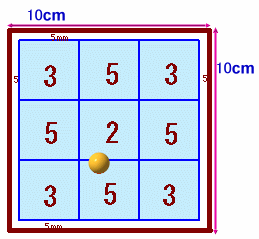
左図のような内のりが１０ｃｍ四方の正方形の木枠の中に、１辺が３ｃｍの正方形をした得点板が９枚敷き詰められています。

この木枠の中に、直径１ｃｍのコインを１枚投げ入れ、コインが触れている全ての得点板の数字の合計をポイントとすることにします。

ポイントが３の倍数となるとき、コインの中心がある場所として考えられる得点板上の点の範囲の面積は全体で何ｃｍ2あるでしょう？

２．解答例１(ミミズクはくず耳さん、長野美光さん、トトロ＠Ｎさん、杉本未来さん、noetherさん、他多数)

ポイントが３の倍数となるのは、

  • ３ポイント

  • ５＋５＋２＝１２ポイント

  • ５＋５＋３＋２＝１５ポイント

の３ケースがあり、それぞれ４カ所存在します。

参考図1

（１）３ポイントの場合

参考図2

コインの中心は、３の得点板内で、かつ隣の５の得点板よりは、コインの半径分の５mm以上離れている必要があるので、上図のように１辺が２．５cmの正方形内にある。

従って面積は、合計２．５2×４＝２５ｃｍ2

（２）１２ポイントの場合

参考図3

コインの中心は、２の得点板内で、隣の５の得点板より５mm以内にあり、かつ３の得点板よりは５mm以上離れている必要がある。
従って、上図のように１辺が５mmの正方形内で円の外側にある。

（３）１５ポイントの場合

参考図4

コインの中心は、５、３、２、５の４つの得点板から5mm以内にある必要があるので、上図のように半径が５mmの円内にある。

（２）１２ポイント、（３）１５ポイントの場合を合成すると、
　１辺５mmの正方形および半径５mmの４分の３円となる。

参考図5

従って、面積は０．５2×４＋０．５2×３．１４×(３/４)×４＝１＋２．３５５＝３．３５５ｃｍ2

以上、合計２５＋３．５５５＝２８．３５５ｃｍ2となります。

　

答：２８．３５５ｃｍ2

以上