第１７９問の解答

１．問題　［場合の数]

問題図
1〜９の数字を書いたカードが１枚ずつあります。
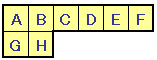
この９枚のカードの中から８枚を選び、左図のような８つの場所に並べて置きます。
このとき、どの隣合う２枚についても、
　・左右では右の方が大きい数字のカード
　・上下では下の方が大きい数字のカード
になるようにします。
このような並べ方は全部で何通りありますか？

２．解答例１(Taroさん、トトロ＠Ｎさん、ちーくん、高橋道広さん、DrKさん、大岡敏幸さん、NobleScaさん、他多数)

数字が１〜８のときを考えます。
左上のＡは、８つの数字の中で最も小さいのでＡ＝１となります。
また、２の数字はＢまたはＧの個所にしか置けません。

参考図1

Ｇ、Ｈには、３〜８の６つの数字から任意の２個を選び、小さい方がＧ、大きい方がＨになります。
また、Ｃ、Ｄ、Ｅ、Ｆの個所には、残った４個の数字を小さい順に並べば良いことになります。

従って、6Ｃ2＝６・５／２＝１５通りとなります。

A=１と同様の理由でＢ＝３は明らかです。

参考図2

Ｈには、４〜８の５つの数字から任意の１個を選べば、2<H、3<Hが成り立ちます。
Ｃ、Ｄ、Ｅ、Ｆの個所には、残った４個の数字を小さい順に並べば良いことになるので、
5Ｃ1＝５通りとなります。

以上から、８個の数字に対して、１５＋５＝２０通りとなります。
ところで、９個の数字から８個を選ぶのに9Ｃ8＝９通りあるので、
全体では、２０×９＝１８０通りとなります。

答：１８０通り

以上

３．解答例２(ミミズクはくず耳さん、ＭＩＬＬさん、他)

解答例１同様、数字が１〜８のときを考え、A=1を得ます。

参考図3

Ｇ、Ｈに２〜８の７個から２個選んだとき、Ｇ＝２、Ｈ＝３は題意を満たしません。

それ以外のときは、残りの５個を小さい順にＢ、Ｃ、Ｄ、Ｅ、Ｆへ並べば良いので、
従って、７Ｃ２−１ ＝ ２０通り 
９枚から８枚選ぶのが９通りなので、合計２０×９＝１８０通り。 

４．解答例３(ヒデー王子さん、noetherさん、他)

縦２×横６の格子上の最短経路(左上から右下に至る)と対応させて考えます。

参考図4

問題図で１から８までの番号を、小さい順にマス目に置いていくので、
　・順路で左から右に進む⇔上側のマス目に入れる
　・順路で上から下に進む⇔下側のマス目に入れる
と対応させることができます。

ただし、×印の個所は題意を満たさないので除きます。
この個所を通らない経路を数え上げると、上図のように２０通りとなります。

以下、同様。