2.解答例1(長野美光さん、小杉原啓さん、Gouさん、トトロ@Nさん、ミミズクはくず耳さん、圭太さん、LIONさん、高橋道広さん、ふじさきたつみさん、sodoさん、BossFさん、有無相生さん、杉本未来さん、中村明海さん、DrKさん、たなかさん、他多数)
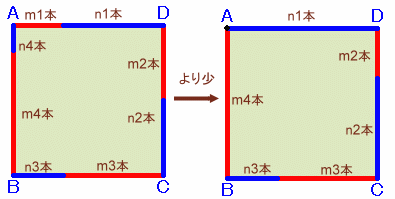
正方形の各辺にある赤い棒、青い棒の本数の合計が最も少なくなるときを下図のようにします。(ただし、m1<m2<m3<m4)
このとき、各辺の長さが等しいことから、n1>n2>n3>n4となります。
もしm1>0とすると、各辺から赤い棒をそれぞれm1本ずつ取り除いても、各辺の長さは等しいので正方形となり、元の正方形より棒の合計本数が少なくなるので矛盾します。よって、m1=0本でなければなりません。
全く同様にして、n1=0本となります。
ここで、赤い棒、赤い棒それぞれ1本の長さをa、bとします。
題意より、a>bとなります。上記より、n1×b=m4×a、
よって、求める比をkとおくと、
k=a/b=n1/m4、
従ってkは有理数となります。kを既約分数にしたものをp/qとおきます。
上図より、
m2×a=(n1-n2)×b ・・・ (1)
m3×a=(n1-n3)×b ・・・ (2)
m4×a=n1×b ・・・ (3)
が成り立ちます。(1)より、n1-n2=m2×a/b=m2×p/q。
n1-n2は整数だから、m2はqの倍数。
同様に、m3、m4もqの倍数。
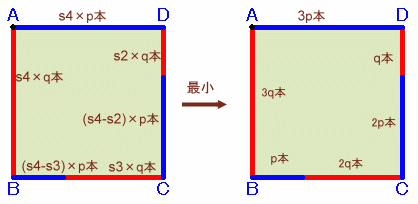
よって、m2=s2×q、m3=s3×q、m4=s4×qとおくことができます。
m2<m3<m4より、s2<s3<s4 ・・・ (7)また、
n3×b=(m4-m3)×a ・・・ (8)
n2×b=(m4-m2)×a ・・・ (9)
n1×b=m4×a ・・・ (10)
が成り立ちます。(6)から、n1=m4×a/b=m4×p/q=(s4×q)×p/q=s4×p。
同様に、n2=(s4-s2)×p、n3=(s4-s3)×p。
(7)より、
1≦s2、2≦s3、3≦s4、1≦s4-s3、2≦s4-s2
従って、棒の本数合計が最小ととなるのは、上の右図のときとなる。
このとき、棒の本数合計=3q+(2q+p)+(q+2p)+3p=6(p+q)=90本。
よって、p+q=15本となります。1<k=p/q<2となる、pとqの組み合わせを求めると、
p/q=8/7、9/6
の2組しかない。
このうち、9/6は既約分数ではないので不適。よって、p/q=8/7のみが題意を満たします。
答:8:7
以上