第１８２問の解答

１．問題　［割合]

濃さ、量ともに等しい食塩水が入った２つの容器A、Bがあります。
Ａには、１４ｇの水を、Ｂには２８ｇの水を入れてうすめたところ、Ａの食塩水２８ｇ中の食塩の量と、Ｂの食塩水３０ｇ中の食塩の量が等しくなりました。
では、最初２つの容器には、何ｇずつの食塩水が入っていたでしょうか？

２．解答例１(小杉原啓さん、萬田銀次郎さん、CRYING DOLPHINさん、トトロ＠Ｎさん、大岡敏幸さん、sodoさん、他多数)

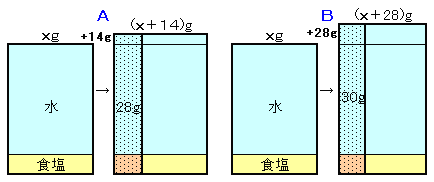
元の食塩水の量をxｇとします。

参考図1

うすめたＡの食塩水２８ｇは、元の食塩水Ａでは、28×x/(x+14)ｇ、
うすめたＢの食塩水３０ｇは、元の食塩水Ｂでは、30×x/(x+28)ｇに相当する。

従って、
　28×x/(x+14)＝30×x/(x+28)
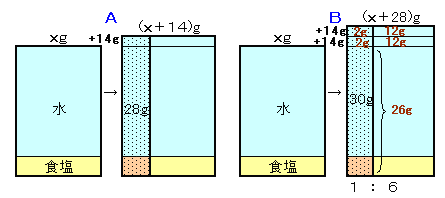
　(x+28)/(x+14)＝30/28
　1+14/(x+14)＝1+2/28
　(x+14)/14＝14
よって。x＝14×14-14＝１８２ｇとなります。
　

答：１８２ｇ

以上

３．解答例２(高橋道広さん、他)

参考図2

うすめた食塩水Ａの２８ｇ中に含まれる食塩と、うすめた食塩水Ｂの３０ｇ中に含まれる食塩の量が等しいことから、増分の差１４ｇは、３０ｇ−２８ｇ＝２ｇと、１４ｇ−２ｇ＝１２ｇに分かれます。

従って、うすめた食塩水Ｂの３０ｇの部分は、うすめる前の食塩水Ｂでは、３０ｇ−（２ｇ＋２ｇ）＝２６ｇに相当します。

うすめた食塩水Ｂで、３０ｇと残りの食塩水の比は、２ｇ：１２ｇ＝１：６となるので、元の食塩水の量は２６×７＝１８２ｇとなります。