第１８５問の解答

---

１．問題　［割合]

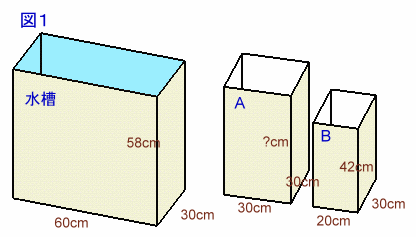
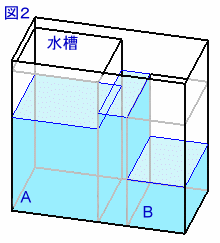
図１のように、水がいっぱいに入った深さ５８ｃｍの水槽と、深さの分からない空の箱A,深さ４２ｃｍの空の箱Bがあります。（箱の厚さは考えません。） この水槽にまず箱Ａをまっすぐに沈め、次に箱Ｂを静かに沈めると図２のように、Ａに入った水の深さがＢに入った水の深さの２倍になりました。 では、Ａの箱の深さは何ｃｍでしょうか。

---

２．解答例１(Hamayanさん、トトロ＠Ｎさん、Gouさん、小杉原 啓さん、有無相生さん、とらいしくるさん、数楽者さん、高橋道広さん、kakeruさん、黒沢宣太郎さん、他)

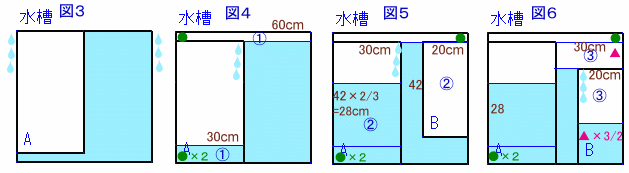
水槽、箱Ａ、Ｂの奥行きは全て３０ｃｍと等しいので、側面の面積で考えれば十分です。

まず箱Ａを沈めていくと、箱Ａの分だけ水は外にあふれ出ます。（図３）
さらに沈めると、箱Ａよりはみ出た部分（�@）が箱Ａに入ってきます。（図４）

このとき、箱Ａの幅と水槽の幅の比は３０：６０＝１：２なので、水の深さの比は２：１。

次に、箱Ｂを沈めていくと、箱Ｂの分だけ水があふれて箱Ａに入ります。（図５）
箱Ａと箱Ｂの幅の比は３０：２０＝３：２、よって水の深さの比は２：３。
従って、箱Ａの水の深さは、４２×2/3＝２８ｃｍ増加します。

さらに、箱Ｂを沈めるとあふれた水が箱Ｂに入ります。
幅の比が２：３だから、水の深さの比は３：２。

従って、水槽と箱Ａの深さの差を●、箱Ａと箱Ｂの深さの差を▲とすると、
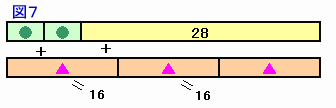
　●×２＋２８＝▲×３／２×２＝▲×３　・・・　（１）
ところが、●＋▲＝水槽と箱Ｂの深さの差＝５８−４２＝１６ｃｍ。　・・・　（２）

図７より、
　▲×３＋▲×３＝（●＋▲）×２＋２８＋▲
　▲×５＝６０
よって、▲＝１２ｃｍ、●＝４ｃｍ。
従って、箱Ａの深さは、５８−●＝５８−４＝５４ｃｍとなります。

あるいは、箱Ａの深さをx cmとおくと、（１）より、
　（５８−x ）×２＋２８＝（x −４２）×３
　５x ＝２７０
よって、　x ＝５４ｃｍ　と解くことができます。

答：５ ４ｃｍ

以上