第１８６問の解答

１．問題　［場合の数]

問題図0

左図のように、碁盤目状の道路があります。
どの道路も南から北方向、西から東方向への一方通行で、かつ「西から東に向かう車が交差点に差し掛かった場合、必ず左折しなくてはならない」という決まりがあります。

（１）Ａから８区間動いてＢに進む方法は何通りありますか。
（２）Ａを出発して８区間動く方法は全部で何通りありますか。
　

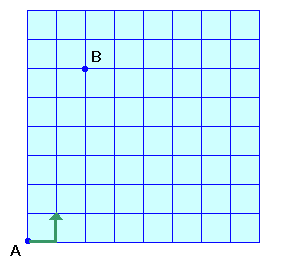２．解答例１(Taroさん、sodoさん、長野美光さん、Gouさん、ミミズクはくず耳さん、杉本未来さん、mhayashiさん、パリンさん、他 多数)

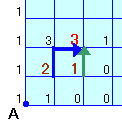
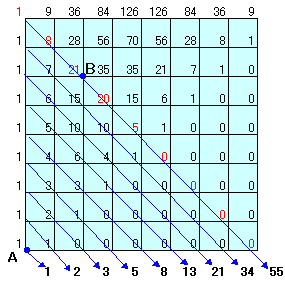
各交差点に、そこまでに至る方法の数を順次書き込んでいきます。

図１
参考図1		 図２
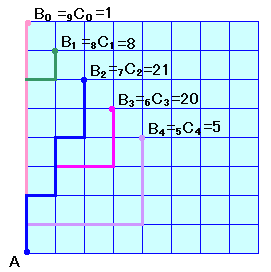
参考図2

Ａからまっすぐ北へ進む場合は、各交差点とも１通り。
Ａからまっすぐ東へ進むと、すぐ右隣は１通りですが、それより東へは行けませんので０通りとなります。

「東へ進むと次は必ず北へ進まなければならない」という条件がなければ、各交差点では、西隣と南隣の交差点上の数を加えればＯＫです。

この条件より、東から来るのは、南西の交差点から進む場合となるので、結局南西および南の交差点上の数を加えていけば良いことになります。（図１）

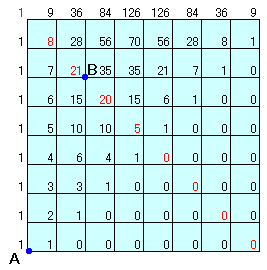
結果は、図２のとおりとなるので、
　（１）ＡからＢへ進むのは、２１通り
　（２）Ａから８区間進むのは、Ｂを含む対角線上の交差点の数を加えて、
　　　１＋８＋２１＋２０＋５＝５５通り
となります。

答：（１）２１通り　（２）５５通り

以上

３．解答例２(トトロ＠Ｎさん、中村明海さん、他)

東西を進む道路を決めれば経路は一意的に決まります。

（１）ＡからＢへ至る経路は、東西の７本の道路から通行する２本を選ぶ場合
　　　の数＝７Ｃ２＝２１通りです。

参考図３


（２）同様に、９Ｃ０＋８Ｃ１＋７Ｃ２＋６Ｃ３＋５Ｃ４
　　　＝１＋８＋２１＋２０＋５＝５５通りです。

参考図４

４．解答例３(Michaelさん、有無相生さん 、他)

参考図５

解答例１の図２を見ると、東西の道路にある交差点上の数字は、下から順に

  • １、１

  • １、２、１

  • １、３、３、１

  • １、４、６、４、１
    ・・・

となり、（x+1）nの係数を並べたもの、いわゆるパスカル三角形をなしていることが分かります。
これは、各交差点上の数字が、すぐ南の道路の隣合う交差点上の数字の和となっているからです。

従って、ｎ番目の対角線上の交差点の数字の和fnは、
　fn＝fn-1＋fn-2
という関係が成り立つのでフィボナッチ数列になります。
８区画進む場合の数は、f9＝５５となります。

（参考）
方角を無視すれば、

  • 北へ１区画進むのを、階段を１つ上る

  • 東へ進み、北へ進むのを、階段２つ上る

とみなして、「階段を１段、または２段ずつ進む場合の数」と同じになることが分かります。

ｎ段の場合を、fnとおけば、

  • 最後を１段上るとき：fn-1

  • 最後を２段上るとき：fn-2

の２ケースに分けられるので、fn＝fn-1＋fn-2が成り立つことが分かります。