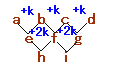第188問の解答
1.問題 [規則性]
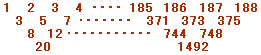 |
|
2.解答例1(ちーくん、AUさん、高橋道広さん、ふじさきたつみさん、まおさん、 他多数)
まず、第n行は、公差2n-1の等差数列になっています。 ・・・ (1)
・第1行は、公差1の等差数列です。
・そして、ある行が公差kの等差数列なら、
上図より、e=a+b、f=b+c、よりf-e=(b-a)+(c-b)=2k となるから、
その次の行は公差2kの等差数列になります。
・よって、帰納法により、(1)が成り立つことが分かります。次に、第3行以下の各数字は、ちょうど真上の数字の4倍になっています。 ・・・ (2)
実際、上図から、
e=a+b、f=b+c、
h=e+f=(a+b)+(b+c)=(a+c)+2b=2b+2b=4b (等差数列だから、2b=a+c)
となります。第2行目までの数字は375以下なので、2001の倍数ではありません。
2001は奇数なので、第n行目(n≧2)までに2001の倍数がないとしたら、
第n+1行目は、第n-1行目の数字の4倍なので、2001の倍数はありません。よって、帰納法により、各行とも2001の倍数がないことが分かります。
答:0個
以上
3.解答例2(ミミズクはくず耳さん、小杉原 啓さん、noetherさん、sodoさん、 DrKさん、有無相生さん、川田智之さん、他多数)
第n行k番目の数字F(n、k)=(n+2k-1)2n-2と表すことができます。・・・ (3)
・第1行:F(1,k)=(1+2k-1)2-1=k となり、(3)は成り立ちます。
・第2行:F(2,k)=(2+2k-1)20=2k+1 となり、(3)は成り立ちます。第n行(n≧2)まで(3)が成り立つとします。
(2)より、
F(n+1、k)
=F(n-1,k+1)・4
=((n-1)+2(k+1)-1)2(n-1)-2・4
=((n+1)+2k-1)2(n+1)-2
となり、第n+1行も(3)が成り立つことが分かります。よって、帰納法により、各行について(3)が成り立つことが分かります。
すると、第n行の数字は、(189-n)個なので、
n+2k-1≦n+2(189-n)=378-n≦377
となり、この中に2001の倍数はありません。
また、2001は奇数なので、2n-2も2001の倍数ではありません。よって、第188行までには、2001の倍数は1個もないことが分かります。
[(3)の別解]
第n行k番目の数字をF(n、k)、および第n行1番目の数字をとくに、G(n)とおきます。
解答例1の(1)より、
F(n、k)=G(n)+(k-1)2n-1 ・・・ (4)
が成り立ちます。また、
G(n+1)=G(n)+F(n、2)=2G(n)+2n-1 ・・・ (5)
G(n+2)=2G(n+1)+2n ・・・ (6)
(6)×2−(5)より、
G(n+2)-2G(n+1)=2G(n+1)-4G(n)
G(n+2)-4G(n+1)+4G(n)=0
従って、G(n)は2階の線形漸化式を満たします。x2-4x+4=0が(x-2)2=0よりx=2を重根として持つことから、
一般式は、 G(n)=(an+b)2n-1と表すことができます。G(1)=a+b=1、G(2)=4a+2b=3より、a=b=1/2を得ます。
従って、G(n)=(n+1)2n-2 となります。(4)より、
F(n、k)=(n+1)2n-2+(k-1)2n-1
={(n+1)+2(k-1)}2n-2
=(n+2k-1)2n-2
となります。