第５問の解答

---

１．問題　［速さの問題］

川を上るときの速さ（静水上での速さ−流れの速さ）が毎分５２５ｍの船があります。この船が、川の上流にある目的地に向かって走っていたのですが、途中で浮き輪を落としてしまいました。 船は浮き輪を落としたことに気づかずにそのまま走り続け、この事故から１５分後にやっと気がついて、すぐに引き返して流れていた浮き輪を 拾い、再度目的地に向かいました。このことで、船は予定より４０分遅く目的地に着いたそうです。 さて、この川は時速何ｋｍの速さで流れているのでしょうか。

---

２．解答例（TORAさん）

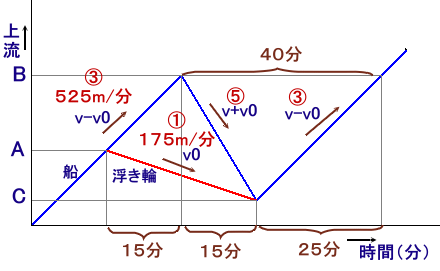
川の流れの速さをv0、静水での船の速さをvとし、
浮き輪を落とした地点をA、気がついた地点をB、浮き輪を拾った地点をCとします。

浮き輪を落としてから気がつく（A→B）まで、船は上流へ(v-v0)の速さで進み、浮き輪は下流へv0の速さで流れていきます。従って、船と浮き輪が遠ざかる速さは、(v-v0)＋v0＝vと静水での船の速さに等しいことが分かります。

同様に気がつくから浮き輪を拾う（B→C）まで、船は下流へ(v＋v0)の速さで進み、浮き輪は下流へv0の速さで流れていきます。従って、船と浮き輪が近づく速さも、(v＋v0)−v0＝vと静水での船の速さに等しくなります。

よって、船がBからCへ上る時間＝AからBへ下る時間＝１５分となります。

船が予定より遅れた４０分は、B→C→Bで発生したことになるので、C→Bの時間＝４０−１５＝２５分となります。

B→CとC→Bの所要時間の比＝１５分：２５分＝３：５だから、
速さの比＝(v＋v0)：(v-v0)＝５：３。

従って、川の流れv0＝（５−３）÷２＝１となります。

船が上る速さ(v-v0)＝５２５m/分なので、川の流れv0＝５２５÷３＝１７５m/分＝１０．５km/時と 求まります。

答：　１０．５km/時

---