第７問の解答

---

１．問題　［平面図形］

クラスの生徒３０人全員が５００円玉を１枚ずつ握りしめて運動場に集まりました。この３０人が、それぞれどの友達とも異なる距離になるようにバラバラに広がります。 この後、それぞれの生徒は自分の持っている５００円玉を自分から一番近くにいる人に渡しました。 このとき、１人に集まる金額は最も多くて何円でしょうか。

---

２．解答例（TORAさん）

最も多く集まった人をAとします。Aは５人からもらうことは可能ですが、６人からは絶対にもらうことはできないことを示しましょう。

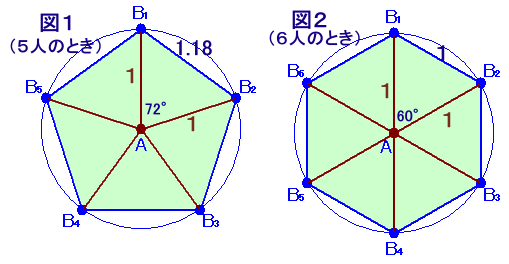
図１のように、Aを中心とする正五角形の頂点のすぐ近くにB₁、B₂、B₃、B₄、B₅の５人がいて、その他の人は全て遠くにいるときを考えます。
B₁〜B₅はAが一番近いので、Aに５００円玉を渡すことになるので、Aはこれらの５人からもらうことになります。

ところが、図２のように正六角形の頂点のすぐ近くにB₁〜B₆の６人がいる場合は、
必ずしもこの６人にとって一番近い人がAとは限りませんので、Aはこの６人からもらうことはできません。

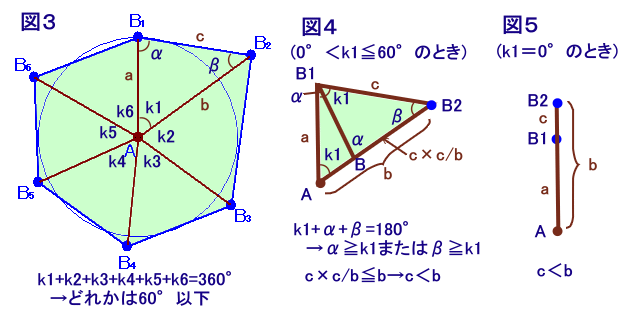
もし、Aが６人からもらうことができるような配置があったとします。（図３）
k₁＝∠B₁AB₂、k₂＝∠B₂AB₃、・・・、k₆＝∠B₆AB₁とし、全て６０°より大きいとします。
 k₁＋k₂＋・・・＋k₆＞６０×６＝３６０°となって矛盾しますので、
少なくとも１個は６０°以下のものが存在します。

これをk₁とし、α＝∠B₁B₂A、β＝∠AB₂B₁、ａ＝AB₁、ｂ＝AB₂、ｃ＝B₁B₂とします。(ただし、k₁＞0)
αもβもk₁より小さいとすると、
　α＋β＋k₁＜k₁×３≦１８０°となって矛盾しますので、
αかβのどちらか一方は、必ずk₁以上になります。

そこでα≧k₁としてみましょう。
AB₂上に点Ｂを、∠B₂B₁Ｂ＝k₁となるようにとると、
△B₁AB₂と△ＢB₁B₂は頂角が全て等しいので相似となります。

よって、
　B₁B₂：ＡB₂＝BB₂：B₁B₂
従って、
　BB₂＝B₁B₂×B₁B₂/ＡB₂＝ｃ×ｃ/ｂ≦ｂ

よって、ｃ²≦ｂ²となり、ｃ≠ｂなので、ｃ＜ｂとなります。
すると、ＡがB₂に一番近いことと矛盾しますので、
背理法によりAが６人からもらうことはできないことが分かります。

以上から、一番多く集まるのは最大５人分＝５００円×５＝２５００円と分かります。

答：　 ２５００円

---