第１２問の解答

---

１．問題　［推理］

０から９までの１０種類の数字を書いたカードを１枚ずつ用意します。 これらのうちの９枚を使って３桁の整数を３個作り、この３つの整数の合計を１９９７になるようにします。 このとき、残された１枚のカードに書かれている数字を答えて下さい。

---

２．解答例（TORAさん）

同じ桁の数字合計について場合分け して考えてみましょう。

１０枚の数字合計＝０＋１＋２＋・・・＋９＝４５
従って、
　残りの１枚＝４５−９枚の数字合計
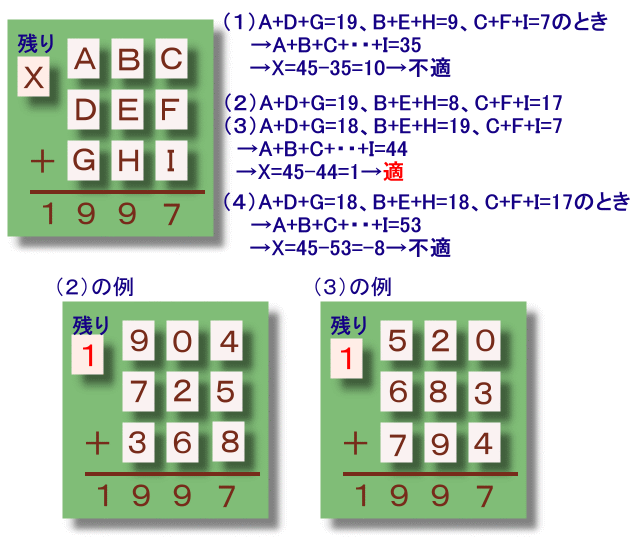
となります。

（ケース１）：Ａ＋Ｄ＋Ｇ＝１９、Ｂ＋Ｅ＋Ｈ＝９、Ｃ＋Ｆ＋Ｉ＝７のとき

９枚の数字合計＝１９＋９＋７＝３５
残り１枚＝４５−３５＝１０　・・・　不適

（ケース２）：Ａ＋Ｄ＋Ｇ＝１９、Ｂ＋Ｅ＋Ｈ＝８、Ｃ＋Ｆ＋Ｉ＝１７のとき

９枚の数字合計＝１９＋８＋１７＝４４
残り１枚＝４５−４４＝１　

例：９０４＋７２５＋３６８＝１９９７・・・　適

（ケース３）：Ａ＋Ｄ＋Ｇ＝１８、Ｂ＋Ｅ＋Ｈ＝１９、Ｃ＋Ｆ＋Ｉ＝７のとき

９枚の数字合計＝１８＋１９＋７＝４４
残り１枚＝４５−４４＝１　

例：５２０＋６８３＋７９４＝１９９７・・・　適・・・　適

（ケース４）：Ａ＋Ｄ＋Ｇ＝１８、Ｂ＋Ｅ＋Ｈ＝１８、Ｃ＋Ｆ＋Ｉ＝１７のとき

９枚の数字合計＝１８＋１８＋１７＝５３
残り１枚＝４５−５３＝−８　・・・　適

以上から、残り１枚の数字は必ず１となることが分かります。

　

答：　 １

---