第１５問の解答

１．問題　［平面図形］

辺の長さが３cm、４cm、５cmの直角三角形のタイルがたくさんあります。
これを隙間なく敷き詰めて菱形を作ります。（正方形は含みません）
このようにしてできる菱形の中で最も小さいものは左図のような菱形です。

では、小さい方から数えて３番目の菱形の面積を求めて下さい。

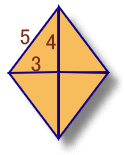２．解答例（TORAさん）

タイル枚数で調べます。

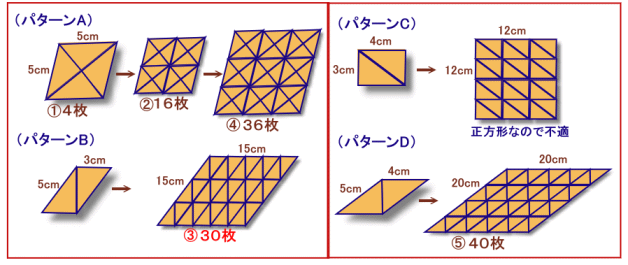
（パターンA）

問題図の菱形を縦横２倍、３倍、・・に拡大しても菱形になります。
このとき、タイル枚数は、４枚、４×２²＝１６枚、４×３²＝３６枚、・・・となります。

従って、３６枚が小さい方から３番目となりそうですが、他のパターンも調べてみましょう。

（パターンB）

タイルを２枚、うち１枚は逆さにして４cmの辺を合わせると、辺の長さが３cm、５cmの平行四辺形になります。
３と５の最小公倍数は１５だから、横５倍、縦３倍に拡大すると辺の長さが１５cmの菱形になります。

このとき、タイル枚数は２×５×３＝３０枚になり、縦横２倍、３倍、・・にすると、
タイル枚数は、３０枚、３０×２²＝１２０枚、３０×３²＝２７０枚、・・・となります。

（パターンC）

タイルを２枚、うち１枚は逆さにして斜辺を合わせると、辺の長さが３cm、４cmの長方形になります。
しかし、これらを横４倍、縦３倍すると正方形となるので、題意に適しません。

（パターンD）

タイルを２枚、３cmの辺を合わせると、辺の長さが４cm、５cmの平行四辺形になります。
４と５の最小公倍数は２０だから、横５倍、縦４倍に拡大すると辺の長さが２０cmの菱形になります。

このとき、タイル枚数は２×５×３＝４０枚になり、縦横２倍、３倍、・・にすると、
タイル枚数は、４０枚、４０×２²＝１６０枚、４０×３²＝３６０枚、・・・となります。

以上から、小さい順に並べてみると、
　４枚、１６枚、３０枚、３６枚、４０枚、・・・
となるので、３０枚が小さい方から３番目と分かります。

このとき、
　菱形の面積＝１/２×３×４×３０＝１８０cm²
と求まります。

答：　１８０cm²