第２１問の解答

１．問題　［平面図形］

問題図

左図で、AB’C’D’は正方形ABCDを頂点Aを中心に３０度反時計回りに回転したものです。

全体（五角形ABCC’D’）の面積が１２３cm2とすると、正方形ABCDの面積はいくらになりますか？。

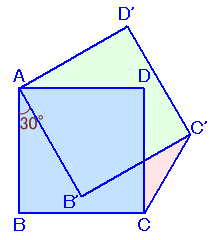２．解答例（TORAさん）

五角形ABCC’D’を線分ACとAC’で３つの三角形に分割して考えます。

参考図１

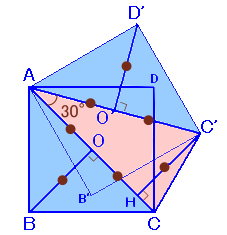
ＡＣの中点をＯ、ＡＣ’の中点をＯ’、Ｃ’からＡＣに下ろした垂線の足をＨとします。

ＡＯ＝ＢＯ＝ＣＯ＝ＡＯ’＝Ｃ’Ｏ＝Ｄ’Ｏより、
　△ＡＢＣと△ＡＤ’Ｃ’は合同となり、面積は等しくなります。

ＡＣ’はＡＣが３０°回転したものなので、∠Ｃ’ＡＣ＝３０°、
よって、Ｃ’Ｈ＝ＡＣ’×１/２＝ＡＯ。

従って、△ＡＣ’Ｃと△ＡＢＣは底辺ＡＣが共通で高さがＢＯ＝ＣＨより、
　面積は等しいことが分かります。

よって、３分割した三角形は全て面積が等しいことが分かります。

従って、△ＡＢＣ＋△ＡＤ’Ｃ’＝正方形ＡＢＣＤ＝１２３cm2
　正方形ＡＢＣＤ＝（△ＡＢＣ＋△ＡＤ’Ｃ’）×２/３＝１２３×２/３＝８２cm2
と求まります。

答：　 ８２cm2