第２４問の解答

１．問題　［場合の数］

ここは遠い未来、冬季五輪高知大会のアイスホッケーの予選組み合わせ抽選会場です。

日本が入った予選Aグループには、日本の他にあと５チームが参加して予選突破を競うことになりました。ただ、日程の関係上各チームの総当たりにすることが難しく、各チームが２試合ずつ試合を行い、その結果で順位を決めることになりました。当然この２試合は異なるチームとの対戦になるようにします。

このような組み合わせの決め方は何通りあるでしょうか？

２．解答例（TORAさん）

各チーム（Ａ、Ｂ、Ｃ、Ｄ、Ｅ、Ｆとします）を●で表し、対戦相手と線で結ぶことにします。

参考図１

どのチームも２試合ずつ行うので●に２本ずつ線があります。
従って、これらをたどっていくとリング状になることが分かります。（途中で止まると、そのチームは１試合になるので）

リングには●と同じだけの線があり、これらは３以上でなければなりません。
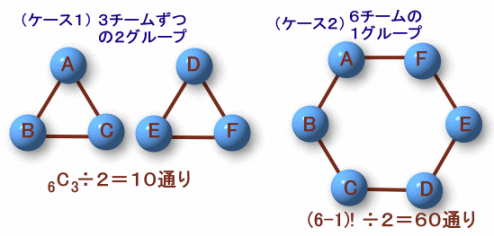
よって、●が３個＋３個の２つのリングに分かれる場合と、●が６個の１つのリングになる２ケースが考えられます。

（ケース１）３個＋３個の２つのリングに分かれる場合

６個から３個を選んでリングを作れば、残りの３個でもう一方のリングが自動的にでき上がります。
従って、6Ｃ3＝２０通りになりますが、２つのリングを交換しても結果は同じ組み合わせになるので、
この半分の１０通りとなります。

（ケース２）６個の１つのリングになる場合

６個の円順列＝（６−１）！＝１２０通りありますが、リングを裏返しにしたものも同じ組み合わせになるので、
この半分の６０通りとなります。

従って、
　合計＝１０＋６０＝７０通り
と求まります。　　

答：　 ７０通り