第２５問の解答

１．問題　［平面図形］

問題図

左図は、正六角形の内側に正三角形２個を書くことによって少し小さめの正六角形を作る作業を３回目まで行ったときの図です。
そして、図のように一番内側を赤色にして、赤色と緑色をまだらに塗り分けることにしました。

この作業を６回目まで続けたとき、赤色の部分と緑色の部分の面積比を求めて下さい。

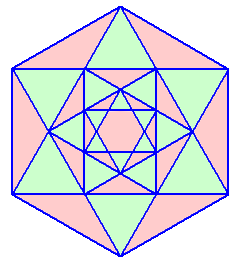２．解答例（TORAさん）

下図は、２回目まで作業したときの図です。

参考図１

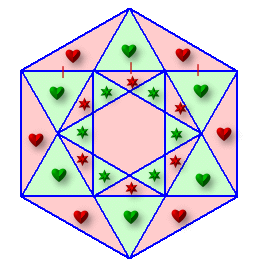
赤色の♥と緑色の♥の、面積は等しく個数も同じです。
また、赤色の★と緑色の★も、同様に面積が等しく個数が同じです。

ということは、赤色の部分と緑色の部分の違いは、中心の正六角形があるかないかだけの違いです。
ここで、中心の正六角形の辺の長さは、元の正六角形の１/３ですから、面積は１/９です。

従って、作業を６回終えた図形を考えると、中心部分は全体の（１/９）3＝１/７２９となることが分かります。

中心の面積を１とすると、全体が７２９ですから、
　赤色＋緑色＝７２９
　赤色−緑色＝１
より、
　赤色＝（７２９＋１）÷２＝３６５
　緑色＝（７２９−１）÷２＝３６４
と求まります。

従って、赤色：緑色＝３６５：３６４と求まります。　　

答：　 ３６５：３６４