第２７問の解答

---

１．問題　［その他］

算チャレVer.2のポイントを獲得しているメンバー全員が一同に集合しました。 集まった人たちには、それぞれ獲得ポイントなどを基準にして順位が付いています。 さて、ここで参加者全員に適当な順で縦１列に並んでもらいました。 そして、自分の後ろに自分より順位が下の人が６人いれば６点、８人いれば８点、 というようにそれぞれ自分の得点を計算します。 一度全員の得点を計算したのですが、列の最後にいたランキング３位のＡさんが 「１番前に行きたい！」というので１番前にいた人と交代しました。 もう一度全員の得点を計算し直すと、合計点は最初と比べて５５点増えていたそうです。 では、最初に１番前にいた人はランキング何位の方だったのでしょうか。

---

２．解答例（TORAさん）

１番前にいてＡさんと交代した人をＸさんとします。

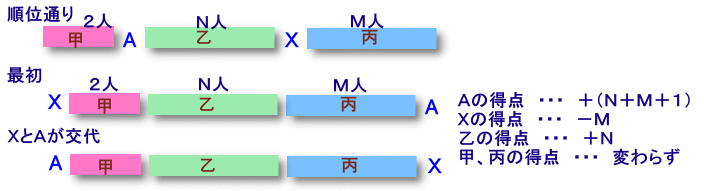
全員を順位通りに並べたとき、

• Ａさんより前の人　　　　・・・　甲グループ （２人）

• ＡさんとＸさんの間の人　・・・　乙グループ （Ｎ人）

• Ｘさんより後ろの人　　　・・・　丙グループ （Ｍ人）

とします。

最初の状態と、XさんとAさんが交代した状態（実際には甲、乙、丙の人が混在しています）を比べてみると、
ＸさんとＡさんが交代することで得点の増減は、

• Ａさん　・・・　０→（Ｎ＋Ｍ＋１）点

• Ｘさん　・・・　Ｍ→０点

• 乙グループ　・・・　各人＋１、合計＋Ｎ点

• 甲、丙グループ　・・・　変わらず

となりますので、全体では、
　＋（Ｎ＋Ｍ＋１）−Ｍ＋Ｎ＝５５点

よって、
　Ｎ＝（５５−１）÷２＝２７人
となります。

従って、Ｘさんの順位は、
　２（甲）＋１（Ａ）＋２７（乙）＋１＝３１位
と求まります。

答：　 ３１位

---