第３０問の解答

---

１．問題　［整数の性質］

A、B、Cの３種類の品物があります。それぞれの値段は、Aが１３７０円、Bが１５３０円、Cが１８７０円です。 ゆたか君はクリスマスプレゼント用に、これらの品物を何個かずつ買ったところ、代金がちょうど３万円になりました。 ゆたか君は、ぞれぞれ何個ずつ買ったのでしょうか。ただし、どの品物も最低１個は買うものとします。

---

２．解答例（TORAさん）

BとCの値段はどちらも１７０円の倍数になるので、Aの値段を１３７０円＝１７０円×８＋１０円と表してみます。

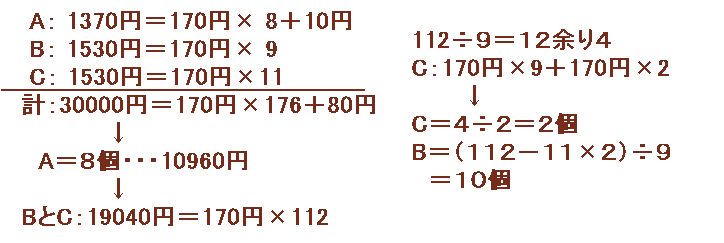
従って、Aの個数は８個、８＋１７個、・・・と考えられますが、３００００円÷１３７０円＝２１．８９...より、Aは２１個以下。
従って、Aは８個と分かります。

３００００円からA×８＝１３７０円×８＝１０９６０円を除くと、ＢおよびＣで１９０４０円＝１７０円×１１２となります。

Ｂ：１７０円×９×Ｂの個数、Ｃ：１７０円×９×Ｃの個数＋１７０円×２×Ｃの個数より、
Ｃの個数は、１１２÷９の余り４の半分＝２個となります。

従って、Ｂの個数＝（１１２−１１×２）÷９＝１０個と分かります。

答：　 Ａ＝８個、Ｂ＝１０個、Ｃ＝２個

---

（参考）式を用いて解く

Ａ、Ｂ、Ｃの個数をｘ、ｙ、ｚとすると、題意より、
　１３７０ｘ＋１５３０ｙ＋１８７０ｚ＝３００００　・・・　（１）
が成り立ちます。

これを変形して、
　（１７０×８＋１０）ｘ＋１７０×９ｙ＋１７０×１１ｚ＝１７０×１７６＋８０
　１７×（８ｘ＋９ｙ＋１１ｚ−１７６）＝８−ｘ

よって、ｎ＝１７６−（８ｘ＋９ｙ＋１１ｚ）とおくと、　・・・　（２）
　ｘ＝８＋１７ｎ
となります。

（１）より、０≦１３７０ｘ≦３００００より、０≦ｘ≦２１．８９...となるので、
　ｎ＝０、ｘ＝８
を得ます。

このとき、９ｙ＋１１ｚ＝１７６−８×８＝１１２。　・・・　（３）
変形して、９（ｙ＋ｚ−１２）＝２×（２−ｚ）

これより、１２−（ｙ＋ｚ）は２の倍数となるので、１２−（ｙ＋ｚ）＝２ｍとおくと、
　ｚ＝９ｍ＋２　・・・　（４）
を得ます。

（３）より、０≦１１ｚ≦１１２となり、０≦ｚ≦１０．１８...となるので、
　ｍ＝０、ｚ＝２
と得ます。

よって。ｙ＝１２−ｚ−２ｍ＝１２−２＝１０となります。

---