第３２問の解答

１．問題　［速さの問題］

問題図

Ａ君とＢ君は仲のよい同級生です。Ａ君の家、Ｂ君の家、学校は左図のようにそれぞれ道で結ばれています。
ある日のこと、二人はそれぞれ３時ちょうどに自分の家を出て、学校の前を通って相手の家に行き、そのまま自分の家まで帰るコースを一定の速度で歩くことになりました。

Ａ君は３時１０分に学校の前でＢ君とすれ違い、３時２８分に再びＢ君とすれ違った後、３時３０分に家に戻りました。

Ｂ君の家から学校まで６００ｍあるとすると、Ａ君とＢ君の家の間の距離はいくらですか？

２．解答例（TORAさん）

２度目に二人がすれ違った地点をPとし、各区間の所要時間を求めると下図のようになります。

参考図１

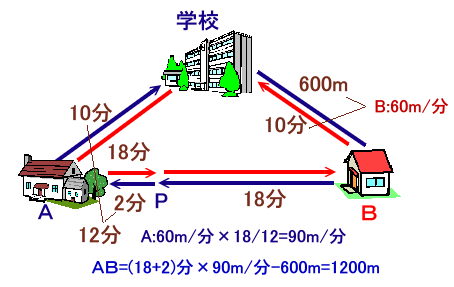
Ｂは、自分の家から学校までの６００mを１０分で歩くのだから、歩く速度は６００m÷１０分＝６０m/分となります。

次に、学校-Aの家-Pを、Bは１８分、Aは２＋１０＝１２分で歩いたのだから、
　Aの速度は、６０m/分×１８/１２＝９０m/分と分かります。

すると、Aは学校-Bの家-Aの家を１８＋２＝２０分歩いたので、この間の距離は９０m/分×２０分＝１８００m、
これから学校-Bの家＝６００mを除くと、Bの家-Aの家の距離は１８００−６００＝１２００mと求まります。

答：　 １２００m