第35問の解答
1.問題 [差集め算?]
|
あるモンスターは戦闘の際、毎分一定量のエネルギーを放出しますが、その一方でこれを一定量だけ補充しながら戦い、エネルギーが無くなれば戦えなくなります。 |
2.解答例1
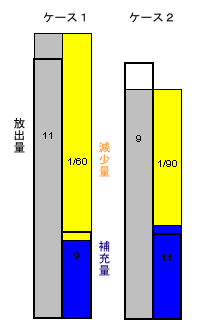

放出量から補充量を引いたものが減少量であり、戦闘可能時間はその逆数である。
ケース1とケース2の平均をとると、放出量・補充量ともに通常と等しいので、減少量・戦闘可能時間も通常と同じになる。従って、通常の減少量=(1/60+1/90)/2=1/72。戦闘可能時間は72分となる。
さて、ケース3では、通常より、減少量は9/10なので、戦闘時間はその逆数10/9となり、通常より72*1/9=8分だけ増える。
以上
3.解答例2
戦闘前のエネルギー量を1として、通常の放出量・補充量・減少量をx、y、z、通常およびケース3の戦闘可能時間をT0、T3とおく。
題意より、
0.9*x−1.1y=1/60、1.1*x−0.9y=1/90、x−y=1/T0、0.9*x−0.9*y=1/T3
となる。
初めの2式より、x=1/48、y=1/144を得る。
従って、x−y=1/72、T0=1/(x−y)=72分、T3=1/((x-y)*0.9)=80分となる。よって、ケース3では、戦闘時間は通常より80−72=8分増えることとなる。
以上