第36問の解答
1.問題 [平面図形・軌跡]
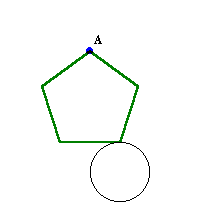
一辺が7cmの正五角形と直径が7cmの円があります。
この円の周りを、正五角形が円に接したまま向きを変えずに(頂点Aを上にしたままで)時計回りに一周します。このとき、頂点Aの動いた距離を求めて下さい。
ただし、円周率は7分の22とします。
2.解答例
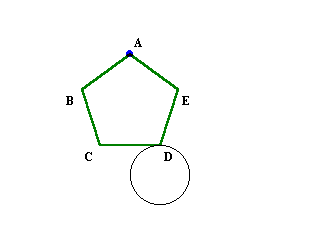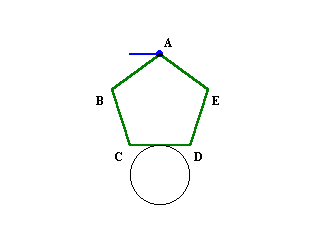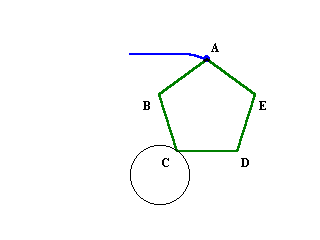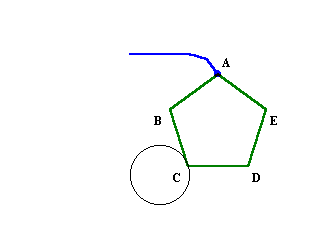
最初に、頂点Dが円の上部と接しているとします。
正五角形が円に接したまま向きを変えずに動かしていくと、辺CDが円に接したまま、頂点Cがちょうど円の上部に来るまで、まっすぐ水平に動くことが分かります。
この間に頂点Aの動いた距離は、DC=7cm。次に、頂点Cが円周に沿って、ちょうど辺BCが円に接するところまで、すなわち5分の1周だけ回ります。
この間に頂点Aの動いた距離は、円周(7π=22)/5=22/5cm。同様にして、正五角形は、CB→BA→AE→EDと順に動いていくことになる。
よって、この間に頂点Aの動いた距離は、(7+22/5)*5=57cm、すなわち正五角形の周の長さと円周の長さの和となる。
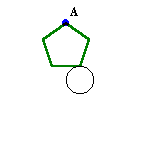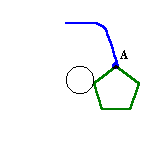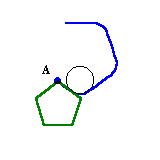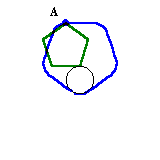
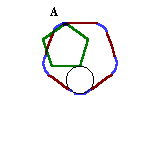
(参考)頂点Aの動く軌跡
茶色の直線:正五角形の辺の長さに等しい
青色の曲線:円周を五分割した長さに等しい
以上