第３８問の解答

１．問題　［整数の性質？］

　ある店では品物の定価に５％の消費税を上乗せした金額を売値とする内税方式をとっています。
　（１円未満の消費税は切り捨て）

　さて、この店の売値の中には存在しない金額があります。

　このような金額は、売値１円～１万円の範囲に何個ありますか。

２．解答例１（ありさのお父さん、わかさひ君、ほそたにさん、ぶぶおパパさん他多数）

・・・

　消費税は、税抜き価格の５％＝１／２０である。

　従って、税抜き価格が１円から１９円までは、消費税は切り捨てて０円だから税込み価格＝税抜き価格である。

税抜き価格が２０円となって、初めて消費税が１円となり、税込価格＝税抜き価格＋１円。

従ってこのとき、税抜き価格の増加がこれまでの１円ずつから２円に変わるので、税込み価格２０円となることはない。

　同様にして、税抜き価格が２０円ごとに１回、いいかえれば税込価格が２１円ごとに１回、存在しない税込価格が出てくることが分かる。

　よって、１万円までに存在しない税込価格の個数は、１００００／２１＝４７６．１９、すなわち４７６個となる。

存在しない税込み価格は上記より、（２１の倍数－１）であり、２０円、４１円、・・・、９９９５円の４７６個である。

あるいは、消費税が１円上がるごとに、１個存在しない税込価格が生じるので、税込み価格１万円のときの消費税が４７６円だから、存在しない税込み価格の個数も４７６個である。

以上

３．解答例２（たなかさん、中村明海さん他）

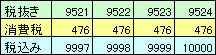
　１００００／１．０５＝９５２３．８１だから、税抜き価格が９５２４円のとき、ちょうど税込価格が１万円となる。

　従って、１万円までの税込み価格のとりうる個数は、税抜き価格が、１円から９５２４円なので、９５２４個以内であるが、税抜き価格が異なれば税込価格も異なるので、結局９５２４個となる。

　従って、存在しない税込価格の個数は、１００００－９５２４＝４７６個となる。

以上