第39問の解答
1.問題 [推理算?]
|
ゆたか君のクラスでは、5人の委員を選ぶことになりました。そこで、全員が投票用紙に、自分自身を含めたクラス全員の中から5人の名前を書いて提出しました。 さて、ゆたか君が全ての投票用紙を調べてみたところ、面白いことに気づきました。どの投票用紙2枚を見比べても、同じ人の名前が1人だけ書かれていたのです。 ゆたか君のクラスの人数は何人なのでしょうか。 |
2.解答例(たなかさん他)
クラスの人数をn人、および題意にある、「どの投票用紙2枚を見比べても、同じ人の名前が1人だけ書かれていた」を投票一致性と呼ぶことにする。
(n>5となること)
5人投票できることから、n≧5である。
もしちょうどn=5とすると、全員が全員に投票することとなり、投票一致性に反するので、n>5となる。(全員が得票数5となること)
もし、全員の得票数が全て4以下とすると、得票数合計はn×4以下となるが、得票数合計は、投票数合計=n×5に等しいので、矛盾する。
よって、得票数は5以上である。得票が6以上の人がいたとする。この人をXとしよう。
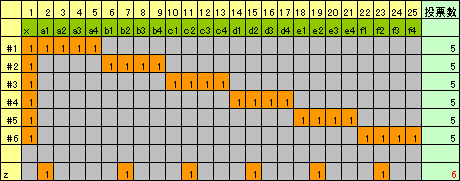
Xに投票した人を#1、#2、#3、#4、#5、#6・・とする。#1から#6のどの2人の投票結果を見ても、投票一致性からX以外の投票結果は全て異なるので、下図のようになる。
さて、もしクラス全員がXに投票したとすると、投票数合計=1+n×4となり矛盾するので、X以外の人に投票した人が必ずいることになる。これを、Zとしよう。
Zは、投票一致性から、a1、・・、a4の中から1人、b1、・・、b4の中から1人、以下同様にして、f1、・・、f4の中から1人投票したことになる。すなわち、投票数が6以上になり、矛盾する。
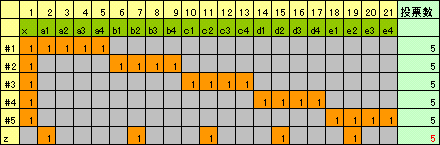
よって、得票数は5以下でなければならず、結局全員の得票数が5となり、下図のようになる。
(クラスの人数が21人となること)
上の図で、投票された人が21人いることになる。
さて、#1から#5以外の任意の人をZとする。
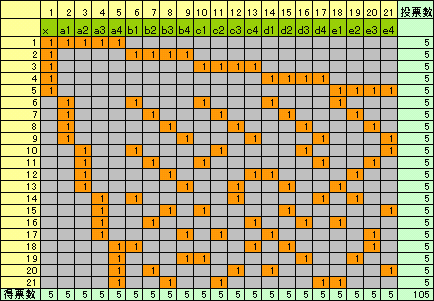
なお、実際に題意を満たす投票結果例として下記のようなものがある。
先ほどと同様に、Zはa1、・・、a4の中から1人、b1、・・、b4の中から1人、以下同様にして、e1、・・、e4の中から1人投票したことになり、これだけで5票となる。
従って、上図にある人以外に投票された人はいないこととなり、クラスの人数は21人と分かる。