第４０問の解答

１．問題　［平面図形］

問題図

左図のように一辺が１８ｃｍの正方形と、その各辺の３等分点を結んで作られた２つの正方形があります。

この図の中心にある八角形の面積を求めて下さい。

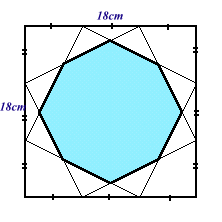２．解答例１（長野義光さん他）

参考図１

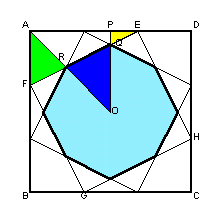左図で、△ＥＰＱと△ＥＡＦは相似だから、
ＰＱ：ＡＦ＝ＥＰ：ＥＡ。
よって、ＰＱ＝ＡＦ×ＥＰ／ＥＡ＝６×３／１２＝１．５ｃｍ。

従って、ＱＯ＝ＰＯ−ＰＱ＝９−１．５＝７．５ｃｍ。

また、△ＯＱＲと△ＡＦＲは相似で、相似比はＯＱ：ＡＦ＝７．５：６＝５：４。

よって、ＲからＯＱへ下ろした垂線の長さは＝ＡＰ×ＯＱ／（ＯＱ＋ＡＦ）＝９×５／９＝５ｃｍ。

従って、△ＯＱＲ＝１／２×７．５×５＝７５／４ｃｍ2。

求める八角形の面積＝△ＯＱＲ×８＝１５０ｃｍ2。


３．解答例２（ありさのお父さん他）

参考図２

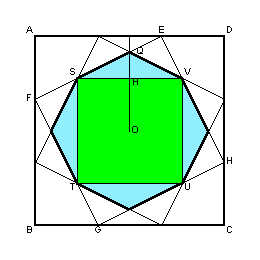左図で、対象性より四角形ＳＴＵＶは正方形で、しかも辺ＳＶは辺ＡＤに平行、辺ＳＴは辺ＡＢに平行となる。
よって、△ＥＳＶと△ＡＥＦは相似な直角三角形となり、正方形ＳＴＵＶと正方形ＥＦＧＨの関係は、正方形ＡＢＣＤと正方形ＥＦＧＨの関係と全く同じになる。

さて、正方形ＡＢＣＤの面積＝１８×１８＝３２４ｃｍ2。
正方形ＥＦＧＨの面積＝正方形ＡＢＣＤの面積×−△ＥＡＦ×４＝３２４−１／２×６×１２×４＝１８０ｃｍ2。

従って、正方形ＳＴＵＶの面積＝正方形ＥＦＧＨの面積×正方形ＥＦＧＨの面積／正方形ＡＢＣＤの面積＝１８０×１８０／３２４＝１００ｃｍ2。

よって、正方形ＳＴＵＶの一辺の長さＳＶ＝１０ｃｍとなる。

従って、ＱＨ＝ＳＨ×ＡＦ／ＥＡ＝１０／２×６／１２＝２．５ｃｍ
よって、△ＱＳＶ＝１／２×ＳＶ×ＱＨ＝１／２×１０×２．５＝１２．５ｃｍ2。

求める八角形の面積＝正方形ＳＴＵＶの面積＋△ＱＳＶ×４＝１００＋１２．５×４＝１５０ｃｍ2。