第４１問の解答

１．問題　［平均？］

　連続した２７個の整数があります。

この２７個を「偶数のグループ」と「奇数のグループ」に分け、それぞれのグループに含まれた整数の合計を比べてみたところ、その差が７４でした。

　では、この２７個の整数の和はいくらでしょうか。


２．解答例１（kuri他）

参考図１

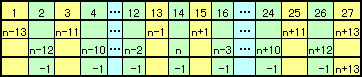
真ん中の数をｎとすると、上図のようになる。

１番目の数と２番目の数、３番目の数と４番目の数、・・・、２５番目の数と２６番目の数の差は、いずれも−１。

従って、２つのグループの整数合計の差は、(n+13)-13＝n＝74。

よって、２７個の整数は、６１，６２，・・・、８７となり、合計は、(61+87)/2×27＝74×27＝１９９８。

３．解答例２（長野義光さん、srtさん他）

参考図２

上図で、対象性より、２つのグループの整数の平均は、それぞれ真ん中の数ｎに 等しい。

よって、差はｎ＝７４。

したがって、整数合計は、ｎ×２７＝７４×２７＝１９９８。