第４３問の解答

１．問題　［規則性・数列？］

　２つのコップに水が入っています。今、量の多いほうからその半分を少ないほうに移します。

　この作業を繰り返し行うと、２つのコップの水の量の差が２１ｃｍ3になり、さらにもう一度作業を行うと２０ｃｍ3になりました。

  1. ２つのコップに入っている水の量は、合わせて何ｃｍ3？

  2. 差が２０ｃｍ3になるまでは、最高で何回の作業を行ったでしょうか？

　

２．解答例１（kuri他）

（水量の合計）

参考図１

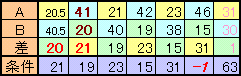
　水量の差が２１ｃｍ3のとき、水量の多いほうをＡ、少ないほうをＢとする。
　一回の操作で、Ａは半分にして、ＢはＡの半分を加えるのだから、その差は、ちょうど操作前のＢの量に等しい。
　すると、Ａの量は、Ｂより差の２１ｃｍ3多い４１ｃｍ3と分かる。よって、水量合計は、４１＋２０＝６１ｃｍ3となる。

（操作を逆にたどる）

参考図2

　差が２１ｃｍ3の一回前の水量は、Ａは今の水量差２１ｃｍ3に等しく、Ｂは今の倍の４０ｃｍ3であり、従って水量差は４０−２１＝１９ｃｍ3となる。
同様にして、Ａ＝４６ｃｍ3、Ｂ＝１５ｃｍ3、差＝３１ｃｍ3まで、さかのぼることができる。
　ところが、同様にその直前の水量を求めると、Ａ＝３１ｃｍ3、Ｂ＝３０ｃｍ3、差＝１ｃｍ3となるが、Ａの水量がＢより多くなるので、操作を逆にはたどれない。
　よって、操作の最高回数は、ここまでの５回である。


（答）： 　（１）６１ｃｍ3 　（２）５回

以上

（補足）操作を逆にたどれるための条件

　操作後の水量をＡ1、Ｂ1、操作前をＡ0、Ｂ0とする。（ただし、Ａ1＞Ｂ1）
すると、　Ａ1＝Ａ0＋Ｂ0×１／２、Ｂ1＝Ｂ0×１／２より、 Ｂ0＝Ｂ1×２、Ａ0＝Ａ1−Ｂ1。
このとき、Ａ0＜Ｂ0でなければならないので、Ａ1−Ｂ1＜Ｂ1×２
よって、Ｂ1×３−Ａ1＞０。

　ところで、さきほどの表に、この条件式を付け加えると下表のようになる。

参考図３

（補足２）一般式を求める

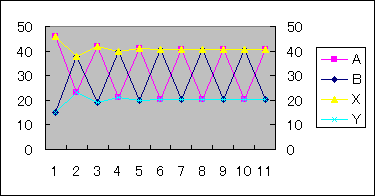
　一番最初の水量をＡ0＝４６、Ｂ0＝１５、Ｚ0＝Ａ0＋Ｂ0＝６１、およびｎ回操作したときの水量をＡｎ、Ｂｎとし、これらのうち、大きい方をＸｎ、小さい方をＹｎとする。

　前述のように、Ｘｎ＋１＝Ｘｎ×１／２＋Ｙｎ、　Ｙｎ＋１＝Ｘｎ×１／２。

　Ｘｎの漸化式を求めると、Ｘｎ＋１＝Ｘｎ×１／２＋Ｚ0−Ｘｎ、すなわち、Ｘｎ＋１＝−Ｘｎ×１／２＋Ｚ0となる。　このとき、Ｘｎの極限値をｘとすると、ｘ＝−ｘ×１／２＋Ｚ0、すなわち、ｘ＝Ｚ0×２／３となる。

　これをもちいて、Ｘｎ＋１−ｘ＝（Ｘｎ−ｘ）×（−１／２）と変形できるので、Ｘｎ−ｘは、公比が（−１／２）の等比数列となり、Ｘｎ−ｘ＝（Ｘ0−ｘ）×（−１／２）ｎ、　よってＸｎ＝（Ｘ0−Ｚ0×２／３）×（−１／２）ｎ＋Ｚ0×２／３と表せる。
　これから、Ｙｎ＝−（Ｘ0−Ｚ0×２／３）×（−１／２）ｎ＋Ｚ0×１／３となる。

　さて、Ａｎ、Ｂｎは、交互に大小が入れ替わるので、 Ａｎ−Ｂｎ＝（Ｘｎ−Ｙｎ）×（−１）ｎであり、Ａｎ＋Ｂｎ＝Ｚ0なので、Ａｎ＝（Ｘ0−Ｚ0×２／３）／２ｎ＋Ｚ0／６×（−１）ｎ＋Ｚ0／２、　Ｂｎ＝−（Ｘ0−Ｚ0×２／３）／２ｎ−Ｚ0／６×（−１）ｎ＋Ｚ0／２となる。

　Ｘ0＝Ａ0＝４６、Ｚ0＝６１を代入して整理すると、Ｘｎ＝１６／３＊（−１／２）ｎ＋１２２／３、Ｙｎ＝−１６／３＊（−１／２）ｎ＋６１／３、Ａｎ＝６１／２＋１６／３＊（１／２）ｎ＋６１／６＊（−１）ｎ、　Ｂｎ＝６１／２−１６／３＊（１／２）ｎ−６１／６＊（−１）ｎとなる。

（参考）

参考図４

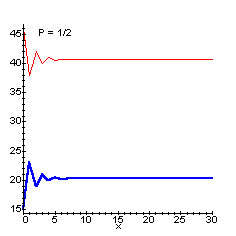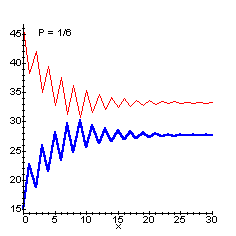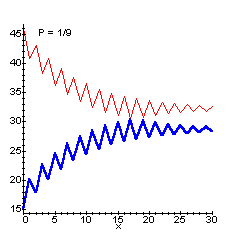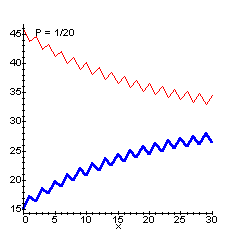
　一般化しよう。一回の作業で多い方のコップから、ｐ倍分（ｐ＜１）だけ少ない方へ移すものとすると、
Ｘｎ＝(61-46*(-1+p)^n*p+31*(-1+p)^n)/(2-p), Ｙｎ＝(61-61*p+46*(-1+p)^n*p-31*(-1+p)^n)/(2-p)　となる。
ｎが大きくなったとき、Ｘｎ、Ｙｎは、それぞれ61/(2-P)、61×(1-p)/(2-p)に収束する。これらの比は、１：（１−ｐ）である。

なお、ｐが1/2から1/20まで変化したときのグラフは以下の通りである。

参考図５（アニメＧＩＦ）