第44問の解答
1.問題 [整数の性質?]
|
和が20になる整数のグループを作ります。例えば、[1,19]や[2,3,4,5,6]などで、個数に制限はありません。 さてここで、グループの整数の最小公倍数をできるだけ大きくしたいと思います。最大でいくらの大きさにできるでしょうか? |
2.解答例(わかさひ君、kuri他)
(補題)
正数X1、X2、・・、Xnは、和がZで一定の時、Y=X1×X2×・・×Xnは、X1=X2=・・=Xn=Z/nのとき最大となる。 相加相乗平均の関係より、(X1+X2+・・+Xn)/n≧(X1×X2×・・×Xn)1/n
よって、X1×X2×・・×Xn≦(Z/n)n(等号は、X1=・・が全て等しいとき)(参考)n=1,2,・・のときの(20/n)nのグラフ
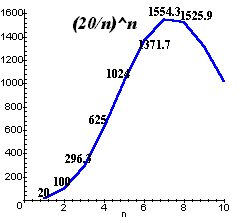
(今回の問題)
今回の問題では、X1、X2、・・、Xnが整数であること、および最小公倍数の最大値を求めることの2つの条件が、補題に加わる。
従って、X1、X2、・・、Xnは、互いに素で、かつなるべく20/nに近い整数を選ぶことが必要となる。
n=4のときを考える。平均値20/4=5に近い整数4個を選んでみると、[3,4,5,6](積:360)、または[4,5,6,7](積:840)が考えられる。
しかし、これらは合計がそれぞれ18,22なので、後者のほうの4と6が互いに素ではないことに注目して、[3,4,5,7](積:420、和:19)を考えてみる。
和が19なので、1を加えて、[1,3,4,5,7](積:420)を一つの候補としてみる。また、n≦3のときは、上記グラフより、420より大きくはならないことが分かる。
n=5のときを考える。平均値20/5=4に近い整数5個を選んでみると、[2,3,4,5,6](積:720)となるが、これらには互いに素でないものが多く含まれている。
そこで、2を1に、6を7に変えてみると、これはn=4のときに考えた[1,3,4,5,7](積:420)に他ならない。さらに、n≧6のときには、平均値がどんどん小さくなって、互いに素なる整数を選ぶことが出来なくなるので、今求めたものが最大となることが分かる。
答:420 以上