第46問の解答
1.問題 [場合の数]
|
52枚のカードがあります。このうち、適当な枚数のカードを使って2人でゲームをします。 互いにカードを取っていき、最後にカードを取る番になったほうが負けです。 ただし、1度に取ることができるカード枚数は、1,3,4枚のいずれかです。 さて、このゲームでは、最初のカード枚数によって、先手必勝か後手必勝かが決まってしまいます。52枚以内で、先手必勝になるカード枚数は、いくとおりあるでしょうか。 |
2.解答例(長野 美光さん、kuri他)
まずカード枚数が、1〜7枚の場合を考えます。
- 1枚のとき: 残ったこの1枚を取らざるを得ないので後手必勝
- 2枚のとき: 1枚取ると残りが1枚となり、相手の手番で後手必勝になるので、結局先手必勝
- 3枚のとき: 2枚は取れないので1枚を取るしかない。このとき、相手番で先手必勝になるので、結局後手必勝。
- 4枚のとき: 3枚とれば1枚残るので、先手必勝。
- 5枚のとき: 4枚とれば1枚残るので、先手必勝。
- 6枚のとき: 3枚とれば3枚残り、相手番で後手必勝になるので、先手必勝。
- 7枚のとき: 4枚とれば3枚残り、相手番で後手必勝になるので、先手必勝。
従って、最初のカード枚数が2,4,5,6,7枚のとき先手必勝、1,3枚のとき後手必勝となります。
同様に、カード枚数が8以上になったときも、7で割った余りが2,4,5,6,7のとき先手必勝、1,3のとき後手必勝となることが次のようにして分かります。
以下、7で割った余りで割り切れるときを考えます。ただし、7で割り切れるときは余り7としました。
(先手番)枚数(7で割った余り)が2,4,5,6,7とします。
- 2のとき: 1枚取ると残り枚数は1になります。
- 4のとき: 3枚とれば残り枚数は1になります。
- 5のとき: 4枚とれば残り枚数は1になります。
- 6のとき: 3枚とれば残り枚数は3になります。
- 7のとき: 4枚とれば残り枚数は3になります。
従って、必ず1,3にして後手番にできます。
(後手番)枚数(7で割った余り)が1,3とします。
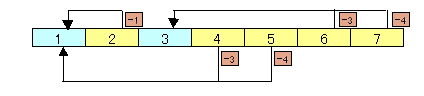
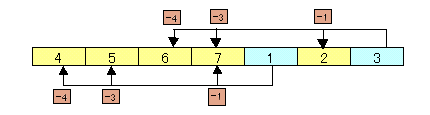
- 1のとき: 1枚取ると残り枚数は7、3枚取ると残り枚数は5、4枚取ると残り枚数は4になります。
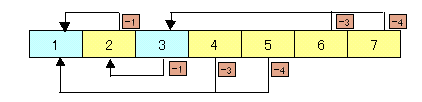
- 3のとき: 1枚取ると残り枚数は2、3枚取ると残り枚数は7、4枚取ると残り枚数は6になります。
従って、どうやっても、先手番に回ったとき、2,4,5,6,7のいずれかになります。
以下、同様にして最後には、枚数が7以下になりますので、結局最初のカード枚数を7で割った余りが2,4,5,6,7のとき先手必勝、1,3のとき後手必勝となります。
さて、52=7×7+3なので、この中に7で割った余りが2,4,5,6,7となるのは、5×7+1=36とおりです。
答:36とおり
以上