第４７問の解答

１．問題　［平面図形］

問題図

　左図は、１辺が６ｃｍの正八角形に、中心からの距離が４ｃｍの直線を２本引いたときの図です。
　この図の下方にある小さな三角形は、直角二等辺三角形になりました。

　さて、この図の色の付いた部分と色の付いていない部分の面積の差は何ｃｍ2でしょうか。

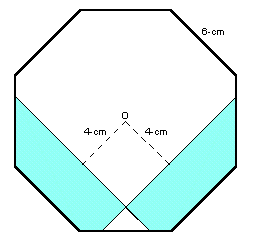
２．解答例（わかさひ君、ありさのお父さん、みのちゃん、kuri他）

参考図１ 参考図２

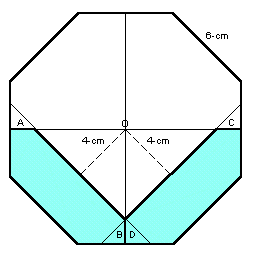
　上左図のように正八角形の中心Ｏを通る垂直および水平な直線を引きます。
　正八角形は、左右および上下に対称ですから、Ａ、Ｂ、Ｃ、Ｄは、全て大きさが同じ直角二等辺三角形になります。
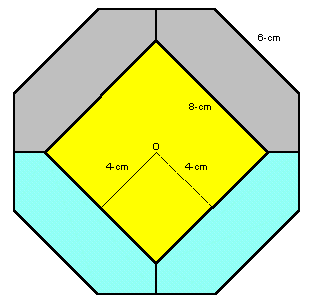
　従って、色の付いた部分の面積は、ＡをＢに、ＣをＤに移した２つの６角形の面積に等しくなります。

　さて、上右図のように正八角形の上部にも同様に２つの６角形（灰色）をつくります。
　すると、青色の部分の面積と灰色の部分の面積は等しくなりますので、求める面積は、真ん中に残った黄色の正方形の面積に等しくなります。

　この正方形の１辺は８ｃｍですので、面積は６４ｃｍ2になります。



答：６４ｃｍ2

以上