第５０問の解答

１．問題　［場合の数］

（１）何人かの人から千円札の寄付を募ります。１人目は、１枚か２枚か３枚かのいづれかの枚数だけ寄付してくれました。
２人目以降の人は、前の人より多くはくれませんでした。この結果、寄付は千円札で３０枚集まりました。
さて、このような寄付の集め方は何通りでしょうか？

（２）集まった３０枚の千円札を、成績優秀者３名に賞金として贈ることにしました。
勿論、２位の人の賞金は、１位の人より多くはなく、３位の人も２位の人より多くはありません。
（ただし、同額であることや、２位や３位が０枚ということも構わないことにします。）
このような配分の仕方は何通りでしょうか？

２．解答例０（あれふさん、ありさのお父さん）

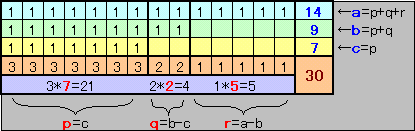
　（１）、（２）の答が同じになることを上図で示します。

　上図のように、７人の人が千円札を３枚、２人の人が２枚、５人の人が１枚寄付してくれたとします。このとき、１位の人に千円札を１４枚、２位の人に９枚、３位の人に７枚、賞金として贈ることが対応します。

　すなわち、一般的に３枚、２枚、１枚だけ寄付した人の数がｐ，ｑ，ｒ（ｐ≧ｑ≧ｒ≧０）に対して、１位の人に（ｐ＋ｑ＋ｒ）枚、２位の人に（ｐ＋ｑ）枚、３位の人にｐ枚贈ることが対応します。
このとき、３×ｐ＋２×ｑ＋ｒ＝３０だから、（ｐ＋ｑ＋ｒ）＋（ｑ＋ｒ）＋ｒ＝３０となります。

　逆に、１位の人にａ枚、２位の人にｂ枚、３位の人にｃ枚、賞金を贈るとするとき（ａ≧ｂ≧ｃ≧０）、３枚寄付した人がｃ人、２枚寄付した人が（ｂ－ｃ）人、１枚寄付した人が（ａ－ｂ）人いることに対応します。
このとき、ａ＋ｂ＋ｃ＝３０だから、３×ｃ＋２×（ｂ－ｃ）＋（ａ－ｂ）＝３０となります。

以上から、（１）、（２）いづれのケースのある場合も他方のケースのある場合に対応するので、（１）、（２）の場合の数は同じである。

３．解答例１：数え上げによる解法（あれふさん、ありさのお父さん他多数）

（１）のケース

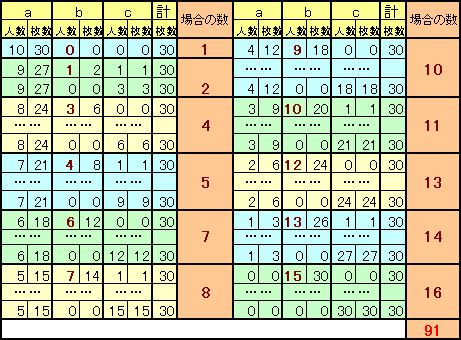
千円札を３枚、２枚、１枚寄付してくれる人数をａ人、ｂ人、ｃ人とする。

ａ（０≦ａ≦３０）に対して、既に３×ａ枚寄付してもらっているので、残りは（３０－３×ａ）枚である。これが、奇数か偶数かによって、ｂのとりうる枚数の上限は異なってくる。そこで、ガウス記号［］（［ｘ］は、ｘを超えない整数で最大のもの。例えば、［１．２］＝１、［２．０］＝２）を使って表すと、ｂの上限＝［（３０－３×ａ）／２］となり、下限は０となる。従って、ｂのとりうる場合の数は、［（３０－３×ａ）／２］＋１となる。

よって、求める場合の数の合計は、これらを加えて、１＋２＋４＋５＋７＋８＋１０＋１１＋１３＋１４＋１６＝９１通りとなる。

答：９１通り

（２）のケース

ｐ（１５≦ｐ≦３０）に対して、既にｐ枚賞金として与えているので残りは（３０－ｐ）枚。
ｑの上限は、（３０－ｐ）枚と容易に分かる。下限のほうは、ｒ＝（３０－ｐ－ｑ）≦ｑとなる必要があるので、［（３０－ｐ）／２］≦ｑより、下限は［（３０－ｐ＋１）／２］と表される。

また、ｐ（０≦ｐ≦１４）のときは、ｑの上限値は、ｐそのものとなり、下限は、上記と同様である。

以上から、場合の数合計は、（１＋１＋・・・＋８＋８）＋（７＋５＋４＋２＋１）＝（１＋８）×８＋１９＝７２＋１９＝９１通りとなる。

答：９１通り

以上

４．解答例２：順列・組み合わせ的解法（中村明海さん他）

ここでは、（２）のケースを賞金合計をｎ枚として、一般的に求めてみることにしましょう。

まず、上位３人Ａさん、Ｂさん、Ｃさんの賞金枚数をａ枚、ｂ枚、ｃ枚として、ａ≧ｂ≧ｃとはいう制限なしでａ＋ｂ＋ｃ＝ｎとなる組み合わせの数を求めます。

これは、３個の異なるものからｎ個とった重複組み合わせになりますので、_{３＋ｎ－１}Ｃ_ｎ＝_ｎ＋２Ｃ_２＝（ｎ＋２）×（ｎ＋１）／２通りになります。（ここの考え方は、例えば白石ｎ個と黒石２個の（ｎ＋２）個を並べ、黒石を仕切りと見て白石を３人に配る配り方から求まります。）

次に、ａ，ｂ，ｃに等しいものがあるかどうかについて場合分けをします。

３つとも等しい：
・ｎが３の倍数のとき　　・・・１通り
・ｎが３の倍数でないとき・・・なし
２つが等しい：
・ｎが３の倍数のとき　　・・・ｍ＝［ｎ／２］とするとき、等しいものの枚数は、０からｍまでの（ｍ＋１）通りから３つ等しい場合を除くので、ｍ通り。等しいものは、ａ，ｂ，ｃから２個選ぶ組み合わせなので３通りあるので、結局ｍ×３通りとなる。
・ｎが３の倍数でないとき・・・ｍ＝［ｎ／２］とするとき、等しいものの枚数は、０からｍまでの（ｍ＋１）通り、等しいものは、ａ，ｂ，ｃから２個選ぶ組み合わせなので３通りあるので、結局（ｍ＋１）×３通りとなる。
全て異なる：
さきほど求めた全組み合わせ数（ｎ＋２）×（ｎ＋１）／２通りから上記２ケースの組み合わせ数を除いたとなる。
・ｎが３の倍数のとき　・・・（ｎ＋２）×（ｎ＋１）／２－１－ｎ×３通り
・ｎが３の倍数でないとき・・・（ｎ＋２）×（ｎ＋１）／２－（ｎ＋１）×３通り

さて、ａ≧ｂ≧ｃの条件を加えた場合と上記の違いを考えると、

３つとも等しい：同じ
２つが等しい：ａ，ｂ，ｃのうち、異なる数は２つで、この中から大きいものをａに制限するのだから上記の３分の１。
全て異なる：ａ，ｂ，ｃが全て異なるので、これらの並び換えの６通りをａ≧ｂ≧ｃに制限するので、上記の６分の１。

よって、求める組み合わせ数は、次のとおりとなる。
・ｎが３の倍数のとき　　・・・１＋［ｎ／２］＋（（ｎ＋２）×（ｎ＋１）／２－１－［ｎ／２］×３）／６＝５／６＋［ｎ／２］／２＋（ｎ＋２）×（ｎ＋１）／１２
・ｎが３の倍数でないとき・・・（［ｎ／２］＋１）＋（（ｎ＋２）×（ｎ＋１）／２－（［ｎ／２］＋１）×３）／６＝１／２＋［ｎ／２］／２＋（ｎ＋２）×（ｎ＋１）／１２

ここで、ｚ（ｎ）＝１（ｎが３の倍数）、０（ｎが３の倍数以外）とおくと、上記式は、
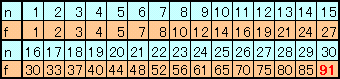
　ｆ（ｎ）＝１／２＋［ｎ／２］／２＋（ｎ＋２）×（ｎ＋１）／１２＋ｚ（ｎ）／３
と表される。

n=1..30

以上