第51問の解答
1.問題 [整数の性質]
5人の人が3桁のある整数について話し合っています。
ところが、5人とも発言の一方は正しく、もう一方は誤りのようです。では、この3桁の整数とは? |
2.解答例1(伏見主事さん、わかさひ君他)
それぞれの人の言ってることを条件1、条件2とすると、Aさんは「条件1が正しくて条件2が誤り」のケースと、逆に「条件1が誤りで条件2が正しい」の2ケースが考えられます。同様に、Bさん、Cさん、Dさん、Eさんについてもそれぞれ2ケース考えられるので、全部で25=32ケースあることになります。
なお、それぞれの条件は、求める整数に1を加えた整数について考えると、2の倍数、3の倍数、・・・、11の倍数となります。
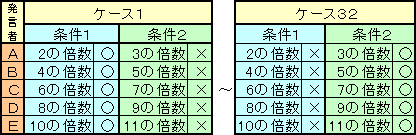
このうち、あり得ないケースを消去していけば良いわけですが、まずCさんの条件1「6の倍数」に着目してみましょう。
もし、条件1が正しいと仮定すると、6の倍数ですから、2および3の倍数にもなります。すると、Aさんの条件1と条件2の両方が正しいことになりますので、6の倍数ではあり得ません。よって、Cさんについては、条件2が正しく、「6の倍数ではなく、7の倍数」ということになります。
さて、今度はDさんに着目してみましょう。
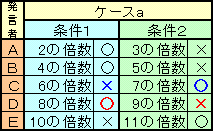
(ケースa)条件1「8の倍数」が正しいと仮定
8の倍数ということは、2の倍数であり、4の倍数でもある。従って、Aさん、Bさんは「条件1が正しく、条件2が誤り」と分かる。
従って、Bさんの条件2が誤りだから5の倍数ではないので、10の倍数でもない。よって、Eさんは、「条件1が誤り、条件2が正しい」ことになる。
(ケースb)条件2「9の倍数」が正しいと仮定
8の倍数でないということは、2の倍数でもなく、4の倍数でもない。従って、Aさん、Bさんは「条件1が誤り、条件2が正しい」と分かる。
従って、Aさんの条件1が誤りだから2の倍数ではないので、10の倍数でもない。よって、Eさんは、やはり「条件1が誤り、条件2が正しい」ことになる。
さて、ケースaの場合、求める整数に1を加えた整数は、2,4,7,8,11の最小公倍数=7×8×11=616の倍数。このうち、3桁の整数は616しかないので、求める整数=616−1=615となる。
次に、ケースbの場合、求める整数に1を加えた整数は、3,5,7,9,11の最小公倍数=5×7×9×11=3465の倍数。このうち、3桁の整数はない。
よって、答はケースaの615のみである。
以上