第５２問の解答

---

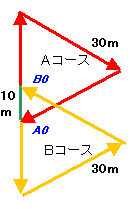
１．問題　［規則性］

左図のような正三角形のコースが２つあります。この２つのコースは、１０ｍ分だけ重なっています。 ゆたか君はＡコースを毎分１９ｍで、ＴＯＲＡさんはＢコースを毎分９８ｍの速さで、それぞれ矢印の方向に回り始めました。 何周かしているうちに、コースの緑色の部分で２人は出会いました。そのあと数分して２人はまた出会いました。 このように２人が出会うことのできる場所は、緑色の部分に最大何カ所あると考えられるでしょうか？

---

２．解答例1（武田 浩紀さん他）

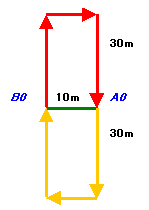
　上記問題図をよく見てみると、次のように変形できます。

図１

→

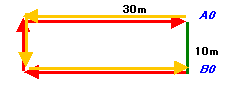
図２

→

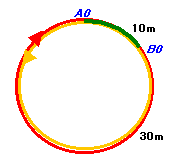
図３

従って、図３の通り周囲３０ｍの円周を、それぞれ向きの異なる方向に回る問題と同等となります。

図４

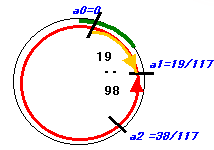
　ゆたか君とＴＯＲＡさんの進む速度の比は１９：９８ですから、最初に出会った地点ａ_０、次に出会った点をａ_１とすると、ａ_０からａ_１までの距離は、円周の１９／（１９＋９８）＝１９／１１７となります。

　同様にして、３度目に出会う地点ａ_２は、ａ_０から１９／１１７×２＝３８／１１７の場所、ａ_３は１９／１１７×３＝５７／１１７・・・、ａ_１１７は１９／１１７×１１７＝１９となり、ちょうどａ_０と同じ地点になります。

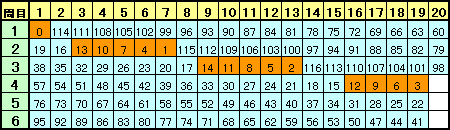
図５

　さて、図５のようにこの間出会う地点は結局ａ_０からスタートして、円周を１１７等分する各点となることが、計算によって分かります。（参考：剰余形による説明）

　さて、緑色の部分は円周の１／９なので、１１７／９＝１３から、ａ_０がちょうど緑色の部分を１３等分する点となるときに１３＋１＝１４地点で出会うことになり、それ以外の時は１３地点なので、結局最大１４地点で出会うことになります。

以上

（参考）剰余形による説明

ｐ_０＝ａ_０を開始点とし、円周を１１７等分する地点をｐ_１、ｐ_２、・・・、ｐ_１１６とします。

ａ_ｎ（０≦ｎ≦１１６）に対し、ａ_０からａ_ｎの距離は、円周の１９／１１７×ｎ倍なので、１９×ｎを１１７で割った余りをｒとすると、ａ_ｎ=ｐ_ｒとなります。

さて、もしａ_ｎ=ａ_ｍ（０≦ｎ＜ｍ≦１１６）となるものがあったとすると、１９×ｎ１９×ｍ（ｍｏｄ　１１７）となります。ところが、１９と１１７は互いに素（１以外の公約数を持たない）ので、ｎｍ（ｍｏｄ　１１７）となりますが、これは０＜ｍ−ｎ＜１１７に反します。

よって、ａ_ｎ（０≦ｎ≦１１６）は全て異なることになるので、｛ａ_ｎ｜（０≦ｎ≦１１６）｝＝｛ｐ_ｎ｜（０≦ｎ≦１１６）｝（集合として一致）になります。

---