第53問の解答
1.問題 [割合?]
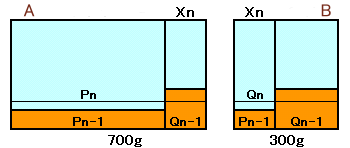
| 5%の食塩水Aが700g、10%の食塩水Bが300gあります。 まず、それぞれの食塩水から10gずつをはかりとり、AからはBへ、BからはAへと、同時に入れ替えます。 次は、20gずつ取り出して入れ替えます。3回目は30gずつ、4回目は40gずつ・・・というように、入れ替える食塩水の量を10gずつ増やしていくと、何回目の作業で2つの食塩水の濃さが等しくなるでしょうか? |
2.解答例1(たなかさん、中村明海さん他)
実は、最後に移し替える食塩水の量は、最初の食塩水A、Bの濃度とは無関係に決まります。
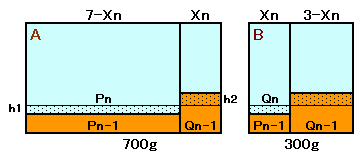
n回目の作業を考えます。移し替える食塩水の量をXn(100gを単位とします。)とし、作業の前に、Aの食塩水の濃度をPn-1%、Bの食塩水の濃度をQn-1%、作業後の濃度をPn%、Qn%とします。
上図の裏塗りをしている部分の面積は等しいので、h1×(7-Xn)=h2×Xnおよびh1×Xn=h2×(3-Xn)となります。これから、(7-Xn):Xn=Xn:(3-Xn)=h2:h1が成り立ちます。従って、(7-Xn)×(3-Xn)=Xn×Xnとなり、これを解いてXn=2.1を得ます。よって、作業1回ごとに食塩水を0.1(×100g)だけ増やすのだから、作業回数n=21となります。
答:21回
以上
3.解答例2(kuri他)
Pn、Qnを一般的に求めましょう。
さきほどの図より、
Pn=(1-Xn/7)×Pn-1+Xn/3×Qn-1 ・・・ (1)
Qn=Xn/3×Pn-1+(1-Xn/3)×Qn-1 ・・・ (2)
となります。(1)×7+(2)×3 および (1)−(2)より、
7×Pn+3×Qn=7×Pn-1+3×Qn-1 ・・・ (3)
Pn−Qn=(1-10/21×Xn)×(Pn-1−Qn-1) ・・・ (4)
を得ます。また、(3)より、
7×Pn+3×Qn=7×Pn-1+3×Qn-1=7×Pn-2+3×Qn-2
=・・・=7×P0+3×Q0=7×5+3×10=65 ・・・ (5)
となります。また、Xn=n/10より、(4)は次のようになります。
Pn−Qn=(21-n)/21×(Pn-1−Qn-1) ・・・ (6)
=(21-n)/21×(20-n)/21×(Pn-2−Qn-2)
・・・
=(21-n)/21×(20-n)/21×・・・×20/21×(P0−Q0)
=20!/(20-n)!/21n×(P0−Q0)
これは、P0−Q0=5−10=−5より
Pn−Qn=−5×20!/(20-n)!/21n ・・・ (7)
となる。ただし、(6)より、n=21のとき、Pn=Qnとなるので、(7)は、n≦20のときまでである。(5)、(7)より、
Pn=(65−15×20!/(20-n)!/21n)/10、
Qn=(65+35×20!/(20-n)!/21n)/10
となります。(n≦20のとき)
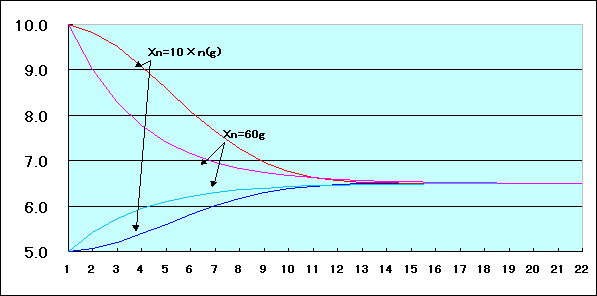
(参考) Pn、Qn、および入れ替える食塩水の量を60gで固定したときのグラフ
以上