第54問の解答
1.問題 [場合の数]
| 1、3、9、27、81・・・のように1とそれに3を何回か掛けてできる数字を書いたカードが1枚ずつあります。 このカードの中から好きな枚数だけとりだしたとき、その合計として作ることのできない3桁の整数は全部で何個あるでしょうか? |
2.解答例1(たなかさん他)
3桁の数字で、カードの組み合わせでできるものを、まず求めることにしましょう。
3のべき乗とその累計を計算します。
![]()
上表から、27までの累計は100未満であり、729までのの累計は1000以上になりますので、一番大きな数字は81、243、729のいずれかです。
- 一番大きな数字が81のとき:
81に1+3+9=13を加えても94<100なので、27は必ず含まれる必要がある。
逆に27が含まれていると、81+27=108>100だから必ず3桁の数字になる。組み合わせは、1、3、9の数字がそれぞれ含まれないか含まれるの2通り×2通り×2通り=8通り。
- 一番大きな数字が243のとき:
最小243、最大364なので全ての組み合わせがOK。
すなわち、1、3、9、27、81の数字がそれぞれ含まれないか含まれるの2通り5=32通り。
- 一番大きな数字が729のとき:
243を含まない場合は、(1+3+9+27+81)+729=121+729=850<1000なので、1、3、9、27、81の組み合わせ32通り。
243を含むと、729+243=972なので、残り加える事が出来るのは999−972=27まで。つまり、1、3、9の組み合わせ8通りと、27の1枚の計9通り。合計32+9=41通り。
以上から、3桁の数字で、カードの組み合わせでできるものは、8+32+41=81通りとなります。
さて、3桁の数字は、100以上999以下の999−100+1=900個ありますので、作り得ない数字は900−81=819個となります。
答:819回
以上
3.解答例2(長野 美光さん、武田 浩紀さん、ありさのお父さん他)
3進数で考えると、カードの組み合わせでできる数字は、各桁の数字が0、1だけでできているものとなります。解答例1同様、これらのうち10進数の100以上999以下のものの個数を求めます。
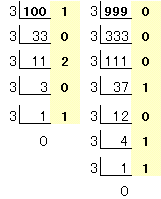
10進数で100、999は3進数で10201および1101000になります。従って、10進数の100以上999以下のものは、3進数で最小11000、最大1101000になります。
ところで、3進数で各桁の数字が0、1だけでできているものの個数は、その各桁の数字でつくる2進数の個数と一致します。
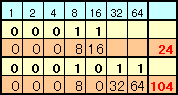
2進数で11000、1101000は10進数では、24、104になりますので、この間の個数は、104−24+1=81個となります。
よって、3桁の数字でカードの組み合わせで作れないものは、900−81=819個となります。
以上